Полная колода карт (52 листа) разбивается наугад на две равные стопки по 26 листов. найти вероятность того, что в одной из стопок не будет ни одного туза.
(введите ответ с точностью до трех знаков после запятой)
Другие вопросы по теме Математика
Популярные вопросы
- Вот это надо ,дополнить предложение правильной формой...
2 - Смешные или грустные рассказы пишет.В.Драгунский...
3 - Какой механизм не используют для подъёма груза?...
2 - Соотнесите произведения искусства и их авторов – титанов ВозрожденияШедевр искусства...
1 - 2 минут 15с ответ сколько секунд...
2 - Во На каком расстоянии должен находится объект от двояковыпуклой линзы, чтобы...
2 - Устройство монивририрывания...
2 - Вырази в указанных един3 ч 15 мин = мин160 мин = Lч мин4ч 50 мин = мин...
2 - заполнить даблицу по произведению Маленький Принц...
1 - Очень мне сейчас уже нужно у выражение (6а/5b) * ( 5b^3/6a)...
1
Количество всевозможных исходов: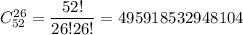
В одной из стопок может быть 4 туза или нет, т.е. в первой стопке - 4 туза, а в другой нет тузов или наоборот. Таких вариантов 2.
Выбрать четыре туза можно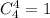 оставшиеся карты без тузов
оставшиеся карты без тузов 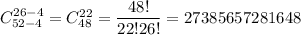 . Всего таких
. Всего таких
Искомая вероятность:
ответ: 0,110.