Почему при последовательном делении числа на 10( примеру,числа abcd), его остатками будет d,c,b,a? в чём принцип? как это доказать? к примеру, число 372 при последовательном делении на 10, в остатках "вернёт" 2 7 3.

Ответы

TheGreatHaterMisha 05.10.2020 09:48

Мы рассматриваем числа в десятичной системе. Это означает, что "цена" разряда - последовательные степени десятки. Например, число из примера можно расписать так:

$\overline{abcd}=a\cdot10^3+b\cdot10^2+c\cdot10^1+d\cdot10^0$

Можно заметить, что все слагаемые в этой сумме, кроме последнего, делятся на 10 (в данном случае второе с конца равно 10c, третье 100b, четвертое 1000a. Но и в общем случае ситуация, очевидно, не меняется).

Остаток от деления натурального числа x на натуральное число y - такое целое число r,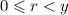 $0\leqslant r$ , что найдётся целое число q, удовлетворяющее равенству 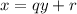x=qy+r . Иначе говоря, (x - r) должно делиться на y.

d - это натуральное число,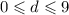 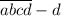$0\leqslant d\leqslant 9$ , $\overline{abcd}-d$ делится на 10, значит, d - остаток от деления исходного числа на 10.

А из того, что

$\overline{\cdots abcd}=\cdots+a\cdot10^3+b\cdot10^2+c\cdot10^1+d=\\=10(\cdots+a\cdot10^2+b\cdot10^1+c\cdot10^0)+d=10\times\overline{\cdots abc}+d$

следует, что после деления на 10 целая часть от деления (q в приведенных выше обозначениях) - это исходное число, но с отброшенной последней цифрой. Для этого числа всё написанное тоже выполняется, поэтому следующий остаток - c, а следующее неполное частное - исходное число без двух последних цифр. Ну и так далее, пока не получится число из одной цифры, она и будет последним остатком, дальше пойдут нули.

Если хочется немного более формального оформления, можете погyглить, что такое принцип математической индукции. По сути, описанное - как раз он, и из него следует, что доказанное утверждение справедливо не только для чисел с не более чем четырьмя цифрами, а вообще для всех натуральных чисел.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика