1. Математика
  2. По формулам смотрел,

По формулам смотрел, так и не разобрался

logangeor logangeor    1   26.12.2019 22:06    0

Ответы
ОTВЕT ОTВЕT  10.10.2020 23:31

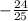
1) -\frac{24}{25}

2) sinα

Пошаговое объяснение:

sin\alpha =\frac{3}{5}

sin2α=2·sinα·cosα

Значит, чтобы вычислит sin2α мы должны определить cosα. Так как π/2 < α < π, то угол α находится во втором квадранте, откуда следует, что знак cosα отрицательный.

cos\alpha =-\sqrt{1-sin^{2} \alpha } =-\sqrt{1-(\frac{3}{5} )^{2} } =-\sqrt{1-\frac{9}{25} } =\\=-\sqrt{\frac{25-9}{25} } =-\sqrt{\frac{16}{25} } =-\frac{4}{5}

Тогда

sin2\alpha=2*sin\alpha*cos\alpha =2*\frac{3}{5} *(-\frac{4}{5})=-\frac{24}{25}

2)

1-2*sin^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )= sin^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )+cos^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )-2*sin^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )=\\=cos^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )-sin^{2}(\frac{\pi}{4} -\frac{\alpha}{2} )=cos2*(\frac{\pi}{4} -\frac{\alpha}{2} )=cos(\frac{\pi}{2} -\alpha )=\\=sin\alpha

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
alex3942 alex3942  27.06.2019 19:40
Почему нельзя сжигать траву на лугах и в других местах? обоснуйте окр мир...
taniamishanina taniamishanina  27.06.2019 19:40
За 1 рейс водитель вывозит 5т тяжелого груза. напиши наименьшее число сколько может сделать рейсов , что бы вывести 48т тяжелого груза?...
NeZoXshock NeZoXshock  27.06.2019 19:40
Участок земли имеет форму прямоугольника,длина которого1,5 км,а ширина составляет 0,6 длины.лес составляет 20% всей площади.определите в гектарах площадь,запятую лесом.....
никита3501 никита3501  27.06.2019 19:40
:девочка израсходовала на покупку 1,3 р., что составило 65% имевшихся у неё денег . сколько денег было ?...
Hhhhhhhhelppppp Hhhhhhhhelppppp  27.06.2019 19:40
Выполнить сложение числа 6 с однозначными числами.выполни сложение. 6+7=(? +? )+(? +)=(? +? )+(? +? )=? ?...
Arx Arx  27.06.2019 19:40
Вкаком лесу темнее в еловом сосновом или смешанном? обоснуйте окр мир...
МисакиКогуна МисакиКогуна  27.06.2019 19:40
Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8+7, то плюс поменяется на минус?...
superscholnik1772 superscholnik1772  27.06.2019 19:40
Вычислите: а)3/5+3/7+9/7*4/15= б)(7/9-1/6): 2/9*21/22= 20 !...
Lraaq Lraaq  27.06.2019 19:40
Выполните деление двумя с объяснение и проверкой 782: 2 984: 3 944: 4 456: 2 543: 3...
ShkolnikN15 ShkolnikN15  27.06.2019 19:40
Нужно решить примеры в столбик 2520: 35 32428: 67 20944: 56...

Популярные вопросы