По данным рисунка найдите высоту трапеции.
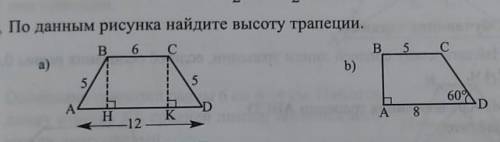
Другие вопросы по теме Математика
Популярные вопросы
- Как решить уравнение 5х+9=43 . подскажите !...
3 - Чему научила меня комедия д.и. фонвизина недоросль...
2 - Религия определяет внутренний мир человека как: а) познание человека...
3 - 1.000 литров бензина стоит 8.500 руб .определите стоимоссть 210литров...
1 - Вшкольную столовую 120кг лука., свеклы-56кг меньше, чем лука, а моркови-в2...
3 - Перевести в двоичную систему восьмеричные числа: 54321,545253,777,1010001...
2 - Правильно составить или поставить do,do not, does в предложения .1....
3 - Играя в прятки со своей подругой,обезьянка пробежала 5 метров по...
3 - Безударные гласные в слове оса, висят, забежало...
1 - Подчеркивай все имена существительные и отмечай слова которые диктуют...
3
Дано, что у нас есть трапеция, для которой мы хотим найти высоту. Высотой трапеции называется отрезок, проведенный перпендикулярно основаниям трапеции и соединяющий эти основания.
Для решения задачи, мы можем воспользоваться знаниями о свойствах трапеции.
Свойства трапеции:
1. Сумма двух пар оснований трапеции равна 1, то есть AC + BD = AB + CD.
2. Высота трапеции разделяет ее на два равных треугольника.
3. В треугольнике со сторонами a, b и c, где сторона a это основание, проведенное противоположно высоте, высота можно найти с помощью формулы: h = (2 * S) / a, где S - площадь треугольника.
Перейдем к решению. Дано, что основание AB равно 13 см, основание CD равно 7 см, а сторона AD равна 8 см.
Сначала, на основании свойства 1, найдем длину основания AC. Используем формулу AC = AB - BD:
AC = 13 см - 7 см = 6 см.
Теперь, используя свойство 2, мы знаем, что высота трапеции разделяет ее на два равных треугольника. Таким образом, треугольник ACD будет равнобедренным.
Мы знаем, что AD = 8 см, а AC = 6 см. Поэтому, чтобы найти высоту треугольника ACD, нам нужно найти длину биссектрисы угла A.
Зная длины сторон треугольника (AD и AC), мы можем использовать формулу для нахождения длины биссектрисы:
BD = (2 * AD * AC) / (AD + AC)
BD = (2 * 8 см * 6 см) / (8 см + 6 см)
BD = (96 см^2) / (14 см)
BD ≈ 6,857 см (округлено до трех десятичных знаков).
Теперь, используя свойство 2, мы знаем, что высота трапеции разделяет ее на два равных треугольника. Таким образом, высота треугольника ACD будет равна высоте трапеции.
Но для того, чтобы найти высоту трапеции, нам нужно знать площадь треугольника ACD. Мы можем использовать формулу для нахождения площади треугольника: S = (1/2) * a * h, где a - одно из оснований треугольника, h - высота треугольника.
Для треугольника ACD, мы можем использовать основание AC и длину биссектрисы BD:
S = (1/2) * AC * BD
S = (1/2) * 6 см * 6,857 см
S ≈ 20,571 см^2 (округлено до трех десятичных знаков).
Теперь мы можем найти высоту треугольника, а следовательно, и высоту трапеции. Используем формулу для нахождения высоты треугольника: h = (2 * S) / a, где a - одно из оснований треугольника.
Мы используем основание AC и площадь треугольника S:
h = (2 * 20,571 см^2) / 6 см
h ≈ 6,857 см (округлено до трех десятичных знаков).
Таким образом, высота трапеции равна примерно 6,857 см.