По данным на рисунках 155, а)—в) вычислите длину стороны треугольника, обозначенной знаком вопроса. При расчетах используйте калькулятор
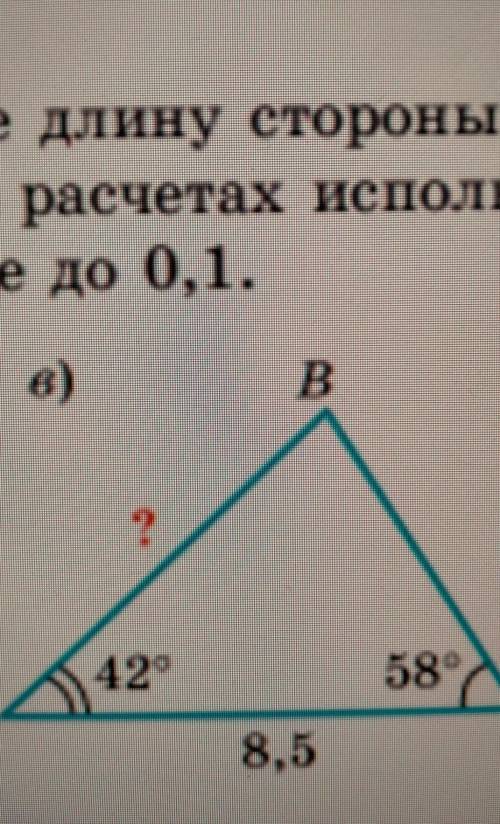
Другие вопросы по теме Математика
Популярные вопросы
- Скласти розповідь про релігію Індійців...
3 - Твір На тему художня література в сучасному світі - необхідність чи пережиток...
3 - Найди и выпиши лишнее слово, не входящее в синонимический ряд. Брякнуть,...
2 - Аксид кальций массе 28г обработали раствор содержит 70г массе азотной...
1 - Знайдіть різницю многочленів 2x+3y та 4х-5y...
3 - Укажите наименьшее общее кратное валентностей химических элементов: Se...
3 - Тапсырмапамагите көмектесші маған жазылуды ұмытпа ...
3 - Выберите верные суждения о правах и обязанностях налогоплательщика. Укажите...
2 - Напишите номер задачи когда будите решать...
3 - Как изменяется средняя температура на острове Биоко...
2
На рисунке 155, а) даны две стороны треугольника: 7 см и 10 см. Давайте обозначим эти стороны как "a" и "b". Мы также видим угол, обозначенный как α, который составляет 30 градусов.
На рисунке 155, б) дана третья сторона треугольника, равная 7 см. Давайте обозначим эту сторону как "c". Мы видим угол, обозначенный как β, который составляет 60 градусов.
Чтобы найти длину стороны треугольника, обозначенной знаком вопроса, мы можем использовать теорему косинусов. Согласно этой теореме, квадрат длины неизвестной стороны равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника на рисунке 155, а), мы можем использовать формулу:
c^2 = a^2 + b^2 - 2ab * cos(α)
Подставим значения a = 7 см, b = 10 см и α = 30 градусов в формулу:
c^2 = 7^2 + 10^2 - 2 * 7 * 10 * cos(30)
c^2 = 49 + 100 - 140 * 0.866 (рассчитаем косинус 30 градусов)
c^2 = 49 + 100 - 121.6
c^2 = 27.4
Теперь возьмем квадратный корень от обеих сторон уравнения:
c = √27.4
c ≈ 5.23 см (с округлением до сотых)
Таким образом, длина стороны треугольника на рисунке 155, а), обозначенная знаком вопроса, примерно равна 5.23 см.
Для треугольника на рисунке 155, б), мы также можем использовать формулу:
c^2 = a^2 + b^2 - 2ab * cos(β)
Подставим значения a = 7 см, b = 7 см и β = 60 градусов в формулу:
c^2 = 7^2 + 7^2 - 2 * 7 * 7 * cos(60)
c^2 = 49 + 49 - 98 * 0.5 (рассчитаем косинус 60 градусов)
c^2 = 49 + 49 - 49
c^2 = 49
Теперь возьмем квадратный корень от обеих сторон уравнения:
c = √49
c = 7 см
Таким образом, длина стороны треугольника на рисунке 155, б), обозначенная знаком вопроса, равна 7 см.
В итоге, для треугольников на рисунках 155, а) и б), мы вычислили длины сторон, обозначенных вопросом. Одна сторона равна примерно 5.23 см, а другая сторона равна 7 см.