Плоскости a и B перпендикулярны. AB перпендикулярно BD, CD перпендикулярно BD, AB = 3, AC = 6, CD = 2 . Найдите длину АС
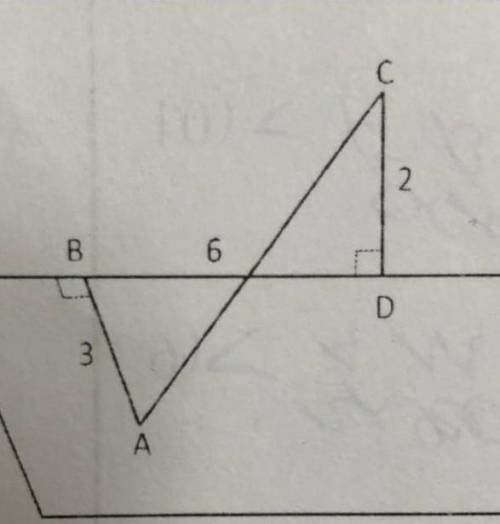
Ответы
Для решения данной задачи мы можем использовать теорему Пифагора и свойства прямоугольных треугольников.
Из условия задачи известно, что плоскости a и B перпендикулярны, а также AB перпендикулярно BD и CD перпендикулярно BD.
Изображение, предоставленное вами, позволяет нам представить данную ситуацию:
A---------------------------B
| |
| |
| |
| C |
|---------------------------|
D
Отсюда следует, что треугольники ABC и ACD прямоугольные, так как AC является гипотенузой данных треугольников (линии, противоположные прямому углу в треугольнике).
Для решения задачи мы можем использовать теорему Пифагора для треугольника ABC.
Согласно теореме Пифагора:
AB² = AC² + BC²
Подставим известные значения в данное уравнение:
3² = 6² + BC²
Упростим уравнение:
9 = 36 + BC²
Вычтем 36 с обеих сторон:
BC² = -27
Видим, что BC² получилось отрицательным числом, что не является корректным.
Это означает, что данные задачи противоречат друг другу и решения нет.
Важно заметить, что при решении задачи используются основные свойства геометрии и алгебры, такие как теорема Пифагора и свойства прямоугольных треугольников. Результат задачи может быть разным в зависимости от данных условий. В данном случае, данные задачи противоречат друг другу и решения нет.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- Найти данный тест полностью, всего вроде бы 32 вопроса должно быть, : ,( 10 класс...
3 - Как называется книжка про apple...
3 - 3. периметр равнобедренного треугольника равен 36 см,основание равно 10 см. найдите...
1 - 1. даны точки а(5; -1) и в(1; 2). найдите координатывектора ab и его модуль.2....
1 - На рисунке дан график зависимости скорости тела массой 3 кг.построить график зависимости...
1 - Втуристическом походе для приготовления чая а на бензиновой горелке вскипятили...
2 - 3complete the text with words fromexercise 1. you do not need all the words.let...
1 - виконайте множення [tex] \frac{x}{6} \times \frac{36}{x {? }^{2} } [/tex]там без...
3 - 15г азотной кислоты растворим в мерной колбе 1 литр, плотность раствора 1,1г/мл.....
3 - Пучок світла падає з повітря на поверхню рідини під кутом 40 градусів кут його...
3