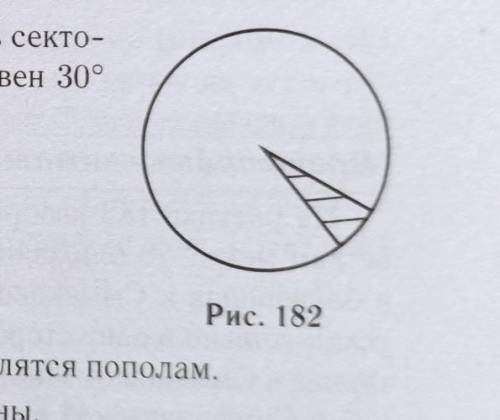
Площадь круга равна 84. Найдите площадь сектора этого круга, центральный угол которого равен 30° (см. рис. 182).​

7

Пошаговое объяснение:

вот таких частей 12 , делим 84 на 12 равно 7

Для того чтобы найти площадь сектора круга, нам нужно знать его площадь и центральный угол.

Сначала найдем радиус круга. Площадь круга выражается формулой S = πr^2, где S - площадь круга, а r - радиус. В данном случае площадь круга равна 84, значит:

84 = πr^2

Далее из этого уравнения можно найти радиус круга r.

Для этого поделим оба выражения на π:

84/π = r^2

Теперь найдем значение r, извлекая корень из обоих частей:

√(84/π) = r

Получаем приближенное значение радиуса круга. Для точности ответа можем оставить его в виде √(84/π).

Теперь мы знаем радиус круга и можем перейти к нахождению площади сектора.

Площадь сектора выражается формулой S = (θ/360) * πr^2, где θ - центральный угол, а r - радиус.

В данном случае центральный угол равен 30°. Подставим значения в формулу:

S = (30/360) * π * (√(84/π))^2

Упростим выражение:

S = (1/12) * π * (84/π)

Сократим π:

S = (1/12) * 84

Выполним умножение:

S = 7

Таким образом, площадь сектора этого круга, центральный угол которого равен 30°, равна 7.