Первый вертолёт пролетел 480 км, а второй --- 800 км. первый вертолёт был в полете на 2 ч меньше чем второй. сколько часов был в полете каждый вертолет, если их скорости были одинаковой?

(1) 800 - 480 = 320 ( км ) - разница

(2) v = s : t = 320 : 2 = 160 ( км / ч ) - скорость каждого вертолета

(3) t = s : v = 480 : 160 = 3 ( ч ) - был в полете первый вертолет

(4) t = s : v = 800 : 160 = 5 ( ч ) - был в полете второй вертолет

Дано:

км

км

\

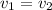
Найти:

Условие задачи можно также представить в виде таблицы (см. рисунок), по которой можно понять, что решить задачу нужно с уравнения.

Формулы, используемые в задаче: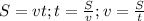

1) Чтобы составить уравнение, нам нужно найти какую-то величину, которая и у I вертолета, и у II вертолёта равна, и это скорость.

Выводим формулы скорости у каждого вертолёта: у первого получится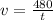 , у второго - 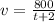(за единицу t мы взяли 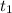, а 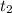представили как t+2.

Получаем уравнение:

Решаем его методом пропорций:

Раскрываем скобки во второй части уравнения:

Перемещаем 480t в первую часть уравнения из второй, меняя при этом знак на противоположный (то есть на минус)

Дальше решаем как стандартное уравнение:

Ура, мы нашли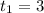 ч. Осталось найти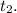

2) Из пункта Дано знаем, что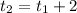 , следовательно:

ч

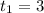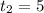ответ: ч; ч