первая труба пропускает на 5 литров воды меньше ,чем вторая. Сколько литров воды в минуту пропускает первая

Question

Математика: первая труба пропускает на 5 литров воды меньше ,чем вторая. Сколько литров воды в минуту пропускает первая труба. если резервуар объёмом 150 литров она заполняет на 10 минут дольше, чем вторая труба резервуар объёмом 75 литров

123456351 · Answer

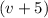Пусть первая труба пропускает литров. Тогда вторая (v+5) л. Если мы вычтем из более производительной трубы мене производительную, то получим время, которое требуется второй трубе, когда первая труба уже заполнила резервуар. Это время по условию равно 10 мин:

$\dfrac{150}{v}-\dfrac{75}{v+5}=10\\\dfrac{30}{v}-\dfrac{15}{v+5}=2\\\dfrac{30(v+5)-15v}{v(v+5)}=2\\30(v+5)-15v=2v(v+5)\\30v+150-15v=2v^2+10v\\2v^2+10v+15v-30v-150=0\\2v^2-5v-150=0\\---\\D=5^2+4 \cdot2 \cdot 150=1225; \qquad \sqrt{D}=35\\v=\dfrac{5+35}{4}=\dfrac{40}{4}=10$