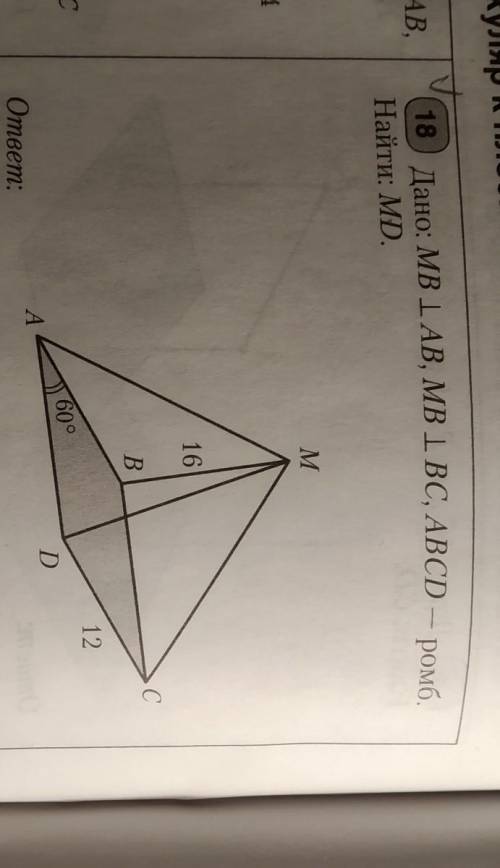
перпендикулярна AB,MB перпендикулярна BC,ABCD-ромб,Найти MD​

Чтобы найти значение MD, мы можем использовать свойства ромба и перпендикуляра. Давайте разберемся пошагово: 1. Сначала вспомним свойства ромба. В ромбе все стороны равны, а диагонали делятся пополам под прямым углом. Таким образом, мы можем сказать, что AB = BC и AC делит MD пополам. 2. Мы знаем, что MB перпендикулярна BC, поэтому у нас есть прямой угол между MD и BC. Из свойств ромба следует, что MD также перпендикулярна AB. 3. Теперь мы можем использовать теорему Пифагора в треугольнике MAB для нахождения значения MD. По теореме Пифагора: (AM)^2 = (AB)^2 + (MB)^2 Мы знаем, что AB = BC (из свойств ромба), а MB перпендикулярна BC (дано в вопросе). Подставим известные значения: (AM)^2 = (BC)^2 + (MB)^2 4. Теперь нам нужно найти значения BC и MB. Мы можем использовать понятие перпендикуляра и прямого угла на основе данных на рисунке. Из рисунка видно, что треугольник AMB прямоугольный. Мы можем применить теорему Пифагора для нахождения значений BC и MB. Положим BC = x и MB = y. (AB)^2 = (AM)^2 + (MB)^2 (x)^2 = (AM)^2 + (y)^2 5. Теперь у нас есть два уравнения: (AM)^2 = (BC)^2 + (MB)^2 (AB)^2 = (AM)^2 + (MB)^2 Подставим выражение для AM из первого уравнения во второе: (AB)^2 = ((BC)^2 + (MB)^2) + (MB)^2 (AB)^2 = (BC)^2 + 2(MB)^2 Теперь мы знаем, что (AB)^2 = (BC)^2 (из свойств ромба). Подставим это в уравнение: (BC)^2 = (BC)^2 + 2(MB)^2 0 = 2(MB)^2 Отсюда следует, что MB = 0. 6. Мы знаем, что AMB прямоугольный треугольник, а MB = 0. Это означает, что угол AMB равен 90 градусам, а значит AM является гипотенузой треугольника. Так как AC делит MD пополам, MD равен 1/2 AC. Вернемся к уравнению (AM)^2 = (BC)^2 + (MB)^2. Так как MB = 0, уравнение упрощается до (AM)^2 = (BC)^2. Это означает, что AM = BC. 7. Мы знаем, что ABCD - ромб, и все его стороны равны друг другу. Мы также знаем, что MD = 1/2 AC. Таким образом, MD = 1/2 BC. Но мы уже установили, что BC = AM. Поэтому MD = 1/2 AM. Мы можем сделать вывод, что значение MD равно половине значения AM. Таким образом, ответ на вопрос будет: MD = 1/2 AM.