1. Математика
  2. Периметри рівностороннього

Периметри рівностороннього трикутника і правильного шестикутника рівні. чому доріню відношення їх площ

danilkatsurkan23 danilkatsurkan23    1   23.10.2019 16:08    0

Ответы
CailiVinchisiter CailiVinchisiter  10.10.2020 09:04

Пусть Р - периметр,

тогда

a=\frac{P}{3}   - длина стороны правильного треугольника;

b=\frac{P}{6}   - длина стороны правильного шестиугольника

S_3=\frac{a^2\sqrt{3}}{4}  - площадь правильного треугольника через его сторону a

S_3=(\frac{P}{3})^2*\frac{\sqrt{3}}{4}=\frac{P^2\sqrt{3}}{36}

S_6=\frac{b^2*3\sqrt{3}}{2} - площадь правильного шестиугольника через его сторону b.

S_6=\frac{P^2*3\sqrt{3}}{6^2*2}}}=\frac{P^2\sqrt{3}}{24}

Найдём отношение площадей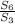  \frac{S_6}{S_3}}:

\frac{S_6}{S_3}=\frac{P^2\sqrt{3}}{24}:\frac{P^2\sqrt{3}}{36}=\frac{P^2\sqrt{3}*36}{24*P^2\sqrt{3}}=1,5

ответ: площадь правильного шестиугольника больше площади правильного треугольника в 1,5 раза.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Марта09 Марта09  12.10.2019 21:10
Периметр квадрата 20 дм. чему равна площадь квадрата? а) 20 дм квадрате, в) 25дм квадрате, с) 20 дм, д) 25 см квадрате...
fsdfsdfdsfsdfsdf fsdfsdfdsfsdfsdf  12.10.2019 21:13
За воскресеньемне просто лень ​...
bogdansudak2006 bogdansudak2006  12.10.2019 21:14
Сколько граммов составляют три четверти килограмма? а) 250 г, в) 800 г, с) 750 г, д) 600...
Vika4634 Vika4634  12.10.2019 21:18
3sin^2 5x+2sin5x*cos5x=2 люди добрые....
student87432467 student87432467  12.10.2019 21:22
Решить! всего-2 карандаша. миша взял 1. сколько осталось карандашей?...
Maryna03 Maryna03  12.10.2019 21:25
1) исследовать на честность y=√x-3 2)найти ооф у=√x^2+4x-2...
minohbli2207 minohbli2207  12.10.2019 19:32
Вам за 305)напишите числа как 0 и напишите неравенство​...
aiis17 aiis17  12.10.2019 19:33
№2 , решите 3 примера ! 15 за это ! прям !...
Daniilkv Daniilkv  12.10.2019 19:33
Мама принесла из инкубатора 56 птенцов,среди которых били цыплята гусята и индюшата.цыплят и гусят вместе было 45 причём гусят было на 4 меньше чем индюшат.сколько было...
спеш спеш  12.10.2019 19:41
Для выполнения проекта «мой город» 1.найти статистические данные по своей теме 2.на основании статистических данных составить 3 3. в группе выбрать форму представления...

Популярные вопросы