1. Математика
  2. Периметр квадрата равен 12см.

Периметр квадрата равен 12см. найдите диагональ квадрата.

rinat0501 rinat0501    2   16.07.2019 18:48    0

Ответы
20yanushkevich04 20yanushkevich04  21.09.2020 12:27

3\sqrt{2}

Пошаговое объяснение:

Найдем сторону квадрата:

P = 4a => a = P/4 = 12/4 = 3

По теореме Пифагора найдем диагональ квадрата:

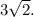
x^{2} = 3^{2} + 3^{2}\\x = \sqrt{18} = 3\sqrt{2}

ПОКАЗАТЬ ОТВЕТЫ
dariababaeva1 dariababaeva1  21.09.2020 12:27

ответ: 3\sqrt{2}.

Периметр квадрата - это сумма длин всех его равных сторон. Так как сторон 4 (пусть каждая из них - а), то формула такая:

Р (периметр) = а + а + а + а = 4а.

Из задачи мы знаем, что:

Р = 4а = 12,        а = 12 : 4,         а = 3.

Теперь мы можем найти диагональ по теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы). Разбиваем квадрат на два прямоугольных треугольника, у каждого из которых катеты равны трем сантиметрам. И теперь мы можем найти гипотенузу - диагональ квадрата:

c = \sqrt{a^{2}+b^{2} } = \sqrt{3^{2}+3^{2} } = \sqrt{9 + 9} = \sqrt{18}=\sqrt{9*2} = \sqrt{9} *\sqrt{2}=3\sqrt{2}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dasha240417 dasha240417  04.02.2021 14:04
с математикой Постройте график функции и Перечислите их свойства​ >...
dianabiran dianabiran  04.02.2021 14:04
Проверь свой глазомер.Можешь ли ты определить какие из отрезков длиннее на каждом из рисунков.Измерь длинны отрезков, в тетради запиши в таблицу и сверь свои предположение...
hhhttt1520 hhhttt1520  04.02.2021 14:04
Умножение десятичной дроби на натуральное число. Умножение десятичных дробей. Урок 3 Из поселка выехал автобус со скоростью 52,5 км/ч. Через 3,2 часа за ним выехал автомобиль...
Русель Русель  04.02.2021 14:03
49. Во вторник в ателье сшили 11 одинаковых курток, а В среду 13 таких же курток. Всего на них израс-ходовали 72 м ткани. Сколько метров ткани израсхо-довали в каждый...
ziatiok2016p074n4 ziatiok2016p074n4  04.02.2021 14:03
Знайдіть довжину відрізка KCна малюнку до попередньої задачі якщо AC 24см pk8 bc15см​...
MDL123 MDL123  04.02.2021 14:03
ПОДПИШУСЬ , И ЗВЕЗДЫ ГЕОМЕТРИЯ 7 КЛАСС ребят, такая тема:решит параллельность​...
burvan1987 burvan1987  04.02.2021 14:03
Найти с какого сайта скачана ​...
ruzannakokh ruzannakokh  04.02.2021 14:03
С2_ас/а2÷c-a/a при а=5, с=26...
stupidgirl3 stupidgirl3  04.02.2021 14:03
Знайдіть х, якщо величини є прямо пропорційними 15 деталей - 3 годХ– 2 годЗнайдіть х, якщо величини є обернено пропорційними3 год - 80 км/год4 год - x​...
Matveykaka Matveykaka  04.02.2021 14:03
Вычислите центральную линию и самое короткое основание одинаковой трапеции, если самое длинное основание составляет 18 см, боковая сторона равна 6 см. Острый угол 60º....

Популярные вопросы