Периметр боковой грани правильной треугольной призмы равен 12 см. При какой длине стороны основания призмы ее объем будет наибольшим?

2

Пошаговое объяснение:

Пусть одна из сторон основания такой призмы - х, и ее высота - h. Тогда периметр ее боковой стороны -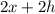 и он равен 12.

Найдем объём такой призмы.

Объем призмы - площадь основания (в данном случае треугольника) умноженный на высоту (h)

Найдём площадь треугольника в основании (см. рис. 1.)

1)  проведём высоту  у. Тогда площадь этого треугольника будет равна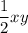

После проведения высоты у нас оказался прямоугольный треугольник со сторонами x и y, и углом между ними в 30°

Тогда его площадь -

Выразим h через х: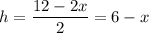

Подставим в формулу объема:

Найдём экстремумы функции:

1)  Найдем производную:

Приравняем её к 0

Поскольку у нас геометрия и таких страшных штук как отрицательные стороны у нас нет. Осталось только выбрать между 2 и 0.

Если 0, то это вообще не призма, знак производной говорит тоже самое.

Тогда подходит 2.

И это ответ!