параметры: найдите наибольшее значение а, при котором уравнение (2а-3)х^4+(а+7)х^2-2а^2-14а=0 имеет единственное решение.

Другие вопросы по теме Математика
Популярные вопросы
- Вгородской библиотеке 14700 книг две седьмых части которых составляет...
1 - Найди значение выражения: 28•7-(32-16): 4+51: 17-1=? , 81: 3+96:...
2 - В5 короб разложили поровну 160 шоколадных конфет сколько конфет...
3 - Скат откладывает 10 яиц а акула в 5 раз меньше сколько яиц откладывает...
3 - Какой частью речи являются данные слова. побег,он,туча,справедливый,бежать,летим...
1 - Мальчик прижал к дну наполненной водой ванны пластмассовый кубик...
1 - Выражение 2/3 (6,9 c - 1 1/2 d ) - 4.8 ( 5/8 c - 2.5 d) ток по подробней...
2 - Как объяснить постановку двоеточия в данном предложении? он чувствовал...
3 - Допиши существительные.укажи их род и число. сладкий,крепкий, сладкая,вкусная,...
3 - А) 17x+5 37x+8 б)6x+9_ x-26. линейное неравенство....
2
Пусть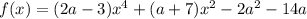
Очевидно, что функция f(x) чётная:
Тогда если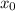 является решение, то и
является решение, то и 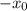 – тоже решение. В таком если случае мы ищем единственное решение, то это только х = 0. Подставим в уравнение:
– тоже решение. В таком если случае мы ищем единственное решение, то это только х = 0. Подставим в уравнение:
Выполним проверку:
Понятно что в этом случае получаем 3 корня, поэтому а = 0 – не подходит. Проверим а = -7:
В этом случае получаем действительно один корень, поэтому а = -7 – подходит.
ответ: а = -7.