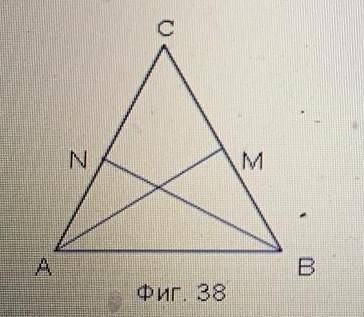
ОТВЕТИТЬ БЫСТРО ЗАДАЧА 1.)АВС равнобедренный треугольник.
АМ и ВN биссектрисы угла.доказать:АМ=ВN
Другие вопросы по теме Математика
Популярные вопросы
- Правописание союзов (также, тоже , чтобы ,причем, притом ,зато)...
1 - Таблица 1941-1945 великая отечественная война. основные битвы.события.дата...
2 - Культура: составить что-то одно : 1. комплекс по оздоровительной аэробике 2.комплекс...
1 - Докажите что произведение в.а.жуковского является . скажите !...
2 - С(2; 3). найти координаты точки а, если в(-1; 2)...
3 - Наспать характеристику василия теркина по плану. 1.портрет. внешний облик,...
3 - Напишите сочинение по рассказу в.распутина ..уроки французкого.. на 2 страницы...
3 - 1после смерти царя федора ивановича,последнего из рюриковичей,новым царём по...
2 - Докажите что произведение жуковского людмила является романом. скажите !...
3 - 1. fill the gaps with reflexive pronouns. ( myself, yourself, himself, herself,...
2
1) Равнобедренный треугольник АВС означает, что стороны АВ и АС равны.
2) Также мы знаем, что AM и BN являются биссектрисами угла А.
3) Согласно свойству биссектрисы угла, она делит противолежащую сторону треугольника на две равные части.
Поэтому мы можем сделать следующие выводы:
АМ равно БМ (по свойству биссектрисы)
АМ равно МС (по свойству биссектрисы)
БМ равно МС (стороны АВ и АС равны)
Общая длина АМ равна сумме длин БМ и МС
АМ равно БМ + МС
BN равно НМ (по свойству биссектрисы)
BN равно НС (по свойству биссектрисы)
НМ равно НС (стороны АВ и АС равны)
Общая длина BN равна сумме длин НМ и НС
BN равно НМ + НС
Теперь мы видим, что обе суммы равны одной и той же величине:
АМ равно БМ + МС
BN равно НМ + НС
Таким образом, АМ равно BN.