ответ:
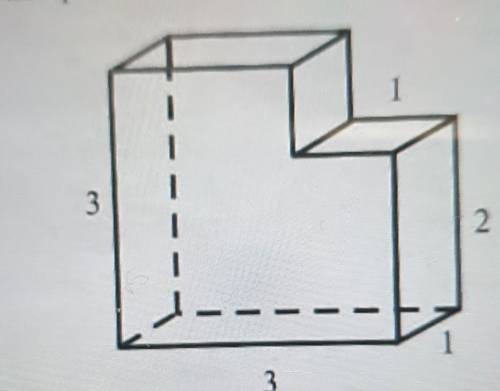
134. Найдите объем фигуры, изображенной на рисунке.

Решение,
ответ:​

Чтобы найти объем фигуры на рисунке, мы должны сначала определить ее форму. Изображение показывает пирамиду с прямоугольным основанием.

Шаг 1: Найдем площадь основания
На рисунке мы видим, что длина основания составляет 8 см, а ширина - 6 см. Чтобы найти площадь прямоугольника, умножим длину на ширину:
Площадь основания = 8 см * 6 см = 48 см²

Шаг 2: Найдем высоту пирамиды
Высота пирамиды не указана на рисунке, поэтому нам нужно использовать геометрические свойства пирамиды. Мы можем представить пирамиду как треугольную призму, где боковые стороны являются равными треугольниками. Таким образом, чтобы найти высоту пирамиды, нам нужно измерить высоту бокового треугольника, изображенного на рисунке.

На рисунке высоту треугольника можно измерить как отрезок, и исходя из рисунка, длина высоты составляет 10 см.

Шаг 3: Найдем объем пирамиды
Мы можем использовать формулу для объема пирамиды: V = (S * h) / 3, где V - объем, S - площадь основания, h - высота.

Вставим значения в формулу:
V = (48 см² * 10 см) / 3 = 480 см³ / 3 = 160 см³

Итак, объем фигуры, изображенной на рисунке, составляет 160 кубических сантиметров (см³).