Отрезок MN имеет длину 18 см. На продолжении отрезка MN за точку N поставили точку P так, что Найти MP
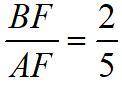
Другие вопросы по теме Математика
Популярные вопросы
- Спутник,вращающийся вокруг земли,перевели на более высокую орбиту.при этом его...
3 - Объясните значение старых слов-коли,потужил,пригорюнился...
3 - Составить уравнения хим реакций и поставить коэффициенты с3н7сооna + naoh= ch3-ch2-ch3+...
2 - Втаблице указана стоимость (в млн рублей) продукции мебельной фабрики за январь,...
2 - Сделайте фонетический разбор слов,используя в случае необходимости орфоэпический...
2 - Склади вираз і знайди його значення. число 6 збільшити на 9,а потімодержане...
1 - 1)определите временную форму сказуемого meine sommerferien habe ich nicht weit...
3 - Решить для 5-го классаистратив 21/34 денег, отведенных на покупку обоев папа...
2 - Объём коробки шириной 2 см длиной 5 см высотой 1 см...
3 - Кто нибудь составить сочинение про лондон что бы я увидел в лондоне когда туда...
3
1. Основное свойство отрезков: отрезок можно продлевать в обе стороны бесконечно.
Исходя из этого свойства, мы знаем, что отрезок MN можно продлить за точку N и получить новый отрезок MP.
2. В треугольнике сумма длин любых двух сторон всегда больше длины третьей стороны.
Исходя из этого свойства, мы можем сформулировать следующую формулу для данной задачи:
MP < MN + NP
Теперь перейдем к решению. У нас есть отрезок MN длиной 18 см. Нам нужно найти длину отрезка MP.
По формуле MP < MN + NP:
MP < 18 + NP
Теперь представим, что длина отрезка NP равна Х см. Тогда формула будет выглядеть следующим образом:
MP < 18 + X
Теперь посмотрим на изображение и задачу. Мы видим, что отрезок MN продлевается за точку N, но предположим, что точка P находится на продолжении отрезка MN внутрь фигуры. То есть, отрезок NP на самом деле является отрезком MP. Тогда можно переписать формулу следующим образом:
MP < 18 + MP
Обратите внимание, что отрезок MP с обеих сторон стоят в одном неравенстве. Это означает, что мы можем упростить его, перенеся его на одну сторону:
0 < 18
Это неравенство всегда будет выполнено, т.к. 0 меньше любого положительного числа, включая 18.
Значит, мы приходим к выводу, что отрезок MP может быть любой длины, больше нуля.