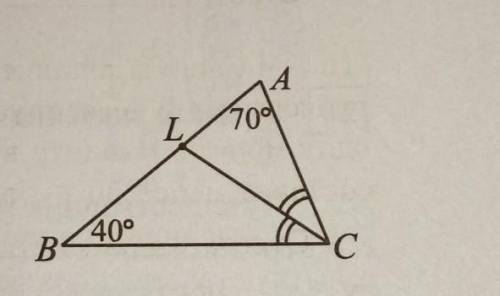
Отрезок CL - биссектриса треугольника ABC. найдите величину угла ALC (в градусах), если известно, что угол А =70 градусам, угол В = 40 градусам

Для решения данной задачи, нам необходимо использовать свойство биссектрисы треугольника.

Биссектриса треугольника делит противолежащий ей угол на два равных угла. В нашем случае, биссектриса треугольника ABC - отрезок CL, который делит угол A на два равных угла, таким образом получается, что угол BCL = угол LCA.

Мы знаем, что угол A = 70 градусов и угол B = 40 градусов. Мы также можем заметить, что угол ALC является дополнительным к углу C, так как они оба образуют прямую линию.

Используя свойства суммы углов треугольника и суммы дополнительных углов, мы можем записать следующее:

Угол A + угол B + угол C = 180 градусов
70 + 40 + угол C = 180
110 + угол C = 180
угол C = 180 - 110
угол C = 70 градусов

Таким образом, мы выяснили, что угол C равен 70 градусов.

Согласно свойству биссектрисы, угол BCL равен углу LCA. Так как угол BCL = 40 градусов, угол LCA также равен 40 градусам.

Итак, величина угла ALC равна углу LCA + углу C = 40 + 70 = 110 градусов.

30 градусов

Пошаговое объяснение: