Отец распределил все свои деньги сыновьям. Соотношение доли младшего сына к доли среднего 2:3, а среднего к старшему 4:5. Если известно, что у отца было 140 млн долларов, то сколько денег получит младший сын?
Другие вопросы по теме Математика
Популярные вопросы
- 1. Укажи неверные утверждения: А. В односоставном предложении второй...
3 - Email письмо другу состоящийся из 80 слов на тему мая местность по английскому...
2 - 6) Сравните информационные объемы, расположив их по возрастанию от самого...
3 - Почвы, формирующиеся под широколиственными лесами: подзолистые, серые...
1 - Предупреждаю вас я, дети, За безопасность вы в ответе.Весной к реке не...
2 - Что общего и в чем различие между изготовления листовых материалов и...
1 - Привет сделать историю, можете рассказать, мне о ОБЩЕСТВО КИТАЯ 18 ВЕК...
2 - Помашите сделайте 3 задание...
1 - Казайық 4. Абай атаның өлеңін оқы. Өлеңдерге ат қой. Мағынасынбойынша...
3 - В выпуклом четырёхугольнике ABCD A = D 90°, C = 90°. Оказалось, что расстояние...
2
32 млн долларов
Пошаговое объяснение:
Пусть старший сын получит х, тогда средний сын получит (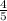 х), а младший сын получит
х), а младший сын получит 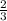 *
* 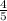 х =
х = 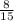 х. Всего было 140 млн. Составим уравнение:
х. Всего было 140 млн. Составим уравнение:
приводим к общему знаменателю
тогда младший сын получил .
.
ответ: младший сын получит 32 млн.
младший сын получил 32 млн долларов
Пошаговое объяснение:
пусть
старший сын получил х млн
средний у млн
младший z млн
теперь составим пропорции, как в условии
отношение доли младшего сына к доли среднего 2:3 это будет
среднего к старшему 4:5
теперь подставим (1) в (2)
а теперь учтем, что у отца было 140 млн, т.е
х +у +z =140
подставим сюда (1) и (3) и получим
решим относительно z
мы получили ответ
младший сын получил 32 млн долларов.