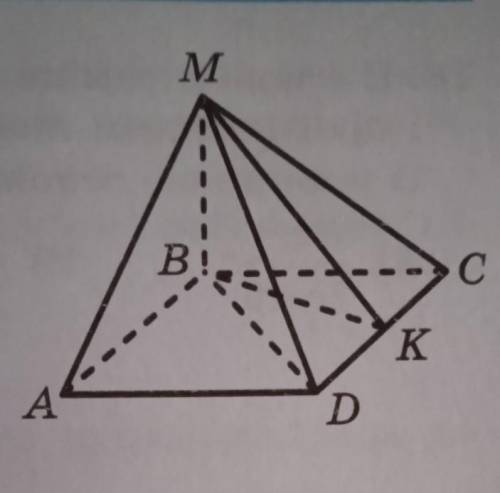
основою піраміди MABCD зображеної на рисунку є квадрат бічне ребро MB перпендикулярне до площини основи піраміди точки K середина відрізка CD укажіть лінійний кут двогранного кута піраміди при ребрі CD​

Добрый день! Рассмотрим данный вопрос пошагово.

1. По условию, мы имеем пирамиду MABCD, у которой основанием является квадрат ABCD, а боковое ребро MB перпендикулярно к плоскости основания и проходит через точку K - середину отрезка CD.

2. Нам требуется найти линейный угол двугранного угла пирамиды при ребре CD. Чтобы понять, что такое линейный угол двугранного угла, нужно вспомнить, что двугранный угол образуется двумя плоскими углами, имеющими общую вершину и общее сторону, которая здесь является ребром CD. Линейным углом двугранного угла называется угол, образованный прямыми линиями, соединяющими вершину угла со всеми точками, лежащими на ребре CD.

3. Так как у нас есть квадрат ABCD, расследуем его свойства. В квадрате все стороны равны, а углы прямые (равны 90 градусам). Также, так как MB перпендикулярно основанию, то оно проходит через точку K, которая является серединой стороны CD, следовательно, сторона KM будет равна стороне KD, и соответственно равна половине стороны CD.

4. Для нахождения линейного угла двугранного угла пирамиды при ребре CD мы должны найти синус угла KMCD. Синус угла можно вычислить, разделив противолежащую сторону на гипотенузу прямоугольного треугольника, образованного этим углом.

5. В данном случае, противолежащей стороной будет сторона KM, а гипотенузой будет ребро CD. Поскольку сторона KM равна половине стороны CD, а сторона CD равна гипотенузе, то синус угла KMCD можно вычислить как (KM / CD) = (0.5 * CD / CD) = 0.5.

6. Таким образом, синус угла KMCD равен 0.5.

7. Для определения значения этого угла по его синусу, можно воспользоваться таблицами тригонометрических функций или калькулятором. В нашем случае, синус угла KMCD равен 0.5, значит значение угла KMCD составляет 30 градусов.

Таким образом, линейный угол двугранного угла пирамиды при ребре CD составляет 30 градусов.