1. Математика
  2. Основание пирамиды-ромб со

Основание пирамиды-ромб со стороной 14 см и острым углом 60 градусов. двугранные углы при основании пирамиды равны 45 градусов. вычислите объём пирамиды.

dflbvdflbv dflbvdflbv    3   01.04.2019 05:00    4

Ответы
двоишник54 двоишник54  28.05.2020 03:02

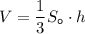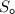Объем пирамиды вычисляется по формуле V=\dfrac{1}{3}S_{\tt o}\cdot h, где S_{\tt o} - площадь основания; h - высота пирамиды.


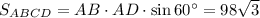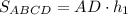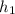Площадь основания равна S_{ABCD}=AB\cdot AD\cdot \sin60^\circ=98\sqrt{3} см², с другой стороны она равна S_{ABCD}=AD\cdot h_1,где h_1 - высота ромба ABCD

Приравнивая площади, получим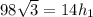 98\sqrt{3}=14h_1 откуда 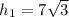h_1=7\sqrt{3} см

Высота ромба является диаметром вписанной окружности, тогда радиус вписанной окружности равен: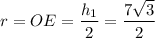 r=OE=\dfrac{h_1}{2}=\dfrac{7\sqrt{3}}{2} см


В прямоугольном треугольнике SOE углы OSE и SEO равны, следовательно ΔSOE - равнобедренный прямоугольный треугольник ⇒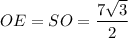 OE=SO=\dfrac{7\sqrt{3}}{2} см



Объём пирамиды: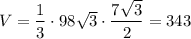 V=\dfrac{1}{3}\cdot 98\sqrt{3}\cdot\dfrac{7\sqrt{3}}{2}=343 см³


Основание пирамиды-ромб со стороной 14 см и острым углом 60 градусов. двугранные углы при основании
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
vesnasurgut vesnasurgut  15.09.2020 17:21
Простым или составным числом будет произведение?17. 1-6. 7 —11. 23 -1. 39 —м.1. 79 —у​...
voronovavlada2 voronovavlada2  15.09.2020 17:20
90км/сағ=?м/с қанша болады? Комектесыныздершы...
5Костя5 5Костя5  15.09.2020 15:59
З пункту А вийшов пішохід. Через 50 хв у тому самому напрямі виїхав велосипедистів і наздогнав пішохода на відстані 6 км від пункту А. Знайти їх швидкості, якщо велосипедист...
nastykatymari nastykatymari  23.09.2019 13:05
Длина баскетбольной площадки 26м а площадь 364м.вычисли шырину площадки...
Salvatation1230 Salvatation1230  23.09.2019 13:05
Решить : за два букета цветов заплатили 240 рублей. в одном букете 7 тюльпанов, а в другом 5 тюльпанов. сколько рублей стоит каждый букет?...
anx2003 anx2003  23.09.2019 13:05
Реши уравнения. ×+7×4=40. 6×3+х=72. 80-х=9×5. 12+х=5×8. х-32: 4=50. х+2×6=94....
sidorova123441 sidorova123441  23.09.2019 13:05
Гелевые ручки в коробках по 8 штук в каждой нужно купить наименьшее возможное число коробок,но так чтобы в них было не менее 350 ручек.сколько ручек было куплено...
ramazan2001xxx ramazan2001xxx  23.09.2019 13:05
Алеша прочитал 24 рассказа ,а костя в 4 раза меньше.сколько всего рассказов прочитали мальчики?...
Unyrfnch Unyrfnch  23.09.2019 13:05
Весь июнь (с 1 по 30 число) сережа читал книги - ровно по 4 страницы в день. но в некоторые дни сережа вообще не читал. оказалось, что число страниц прочитанных серёжей,...
Ketrin2316 Ketrin2316  23.09.2019 13:05
А) (8м 2 дм-43дм 6 см)*70--в метрах и дециметрах б) (6ч 32мин+18ч 7мин) : 17--в часах и минутах...

Популярные вопросы