1. Математика
  2. опрелелите вид треугольника

опрелелите вид треугольника авс, если а(4;2) , b(0;6) c(3;9)

Kroq123 Kroq123    1   02.02.2022 12:55    4

Ответы
ekarerinazak05 ekarerinazak05  02.02.2022 13:00

Найдём длину каждой стороны этого треугольника.

A(4;\,2)\\B(0;\,6)\\C(3;\,9)AB = \sqrt{\left(x_B-x_A\right)^2 + \left(y_B-y_A\right)^2}= \sqrt{\left(0 - 4\right)^2 + \left(6 - 2\right)^2} = \sqrt{\left(-4\right)^2 + 4^2} == \sqrt{16 + 16} = \sqrt{32} = \boldsymbol{4\sqrt{2}}BC = \sqrt{\left(x_C - x_B\right)^2 + \left(y_C - y_B\right)^2} = \sqrt{\left(3 - 0\right)^2 + \left(9-6\right)^2} = \sqrt{3^2 + 3^2} == \sqrt{9 + 9} = \sqrt{18} = \boldsymbol{3\sqrt{2}}

AC = \sqrt{\left(x_C-x_A\right)^2 + \left(y_C - y_A\right)^2} = \sqrt{\left(3 - 4\right)^2 + \left(9 - 2\right)^2} = \sqrt{\left(-1\right)^2 + 7^2} == \sqrt{1 + 49} = \sqrt{50} = \boldsymbol{5\sqrt{2}}

Чтобы определить вид треугольника, нам надо определить вид наибольшего угла этого треугольника. Наибольший угол в треугольнике всегда лежит напротив его наибольшей стороны, поэтому расписываем теорему косинусов для стороны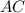 AC:

AC^2 = AB^2 + BC^2 - 2\cdot AB\cdot BC\cdot\cos B2\cdot AB\cdot BC\cdot\cos B = AB^2 + BC^2 - AC^2cos B = \dfrac{AB^2 + BC^2 - AC^2}{2\cdot AB\cdot BC} = \dfrac{32 + 18 - 50}{2\cdot 4\sqrt{2}\cdot 3\sqrt{2}} = \dfrac{0}{48} = 0

Если косинус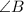 \angle B равен 0, значит, этот угол прямой. Отсюда делаем вывод, что треугольник с заданными точками является прямоугольным.

ответ: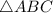 \bigtriangleup ABC - прямоугольный.


опрелелите вид треугольника авс, если а(4;2) , b(0;6) c(3;9)
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Торт123 Торт123  17.05.2019 19:20
Шестой класс найдите корни уравнений 2. 1/6х+1,5=х 3. 1/х+2 = 0,9/5,4 х/у - дробь обыкновенная...
Sashakkkkkkk Sashakkkkkkk  17.05.2019 19:20
Найдите разность чисел 23 и 37 ответы: а)60 б)-60 в)-14 г)14...
PatrickKKK PatrickKKK  17.05.2019 19:20
На поляне ослы и дети.если на каждого осла сядут по одному ребёнку, то двум не хватит осла, а если по 2 ребёнка, то 1 осёл будет лишним. сколько ослов; детей?...
Vceohenploxo Vceohenploxo  17.05.2019 19:20
Запиши частное в виде дроби и выдели из нее целую часть 35: 9=...
незнайка1162 незнайка1162  17.05.2019 19:20
Іть зробити .футбольним м яч коштуе 48 грн.нудільна знижка у магазині складае 3-100ихвід ціни товару.знайди цину м яча після знижки...
Alikman123 Alikman123  17.05.2019 19:20
Что больше 6км 300 м или 6 км 030м 6сут. 14 ч или 7сут. 2 ч 40мин или 1 ч 50мин 8 м 15дм или 8 м 50см 3 т 4 ц или 3 040 кг нужны переводы...
Thrillgang Thrillgang  17.05.2019 19:20
На полках аптеки голубые шары стояло 370 пузырьков маленьких на 25 больше,чем больших а самых маленьких на 127 меньше чем маленьких.сколько самых маленьких пузырьков стояло на...
renatadautova renatadautova  17.05.2019 19:20
Площадь прямоугольника равна 32 дм в квадрате,ширина 4дм.найдите длину и периметр прямоугольника....
summani2005 summani2005  17.05.2019 19:20
Запишите дробь,которая дополняет 1 данную дробь: 4/9,2/7, 5/6,3/5,3/4,7/8....
terehovakira terehovakira  17.05.2019 19:20
Длина сада прчмоугольной формы 30 метров. чтобы сделать забор вокруг сада понадобилось 100 метров. найди ширину этого сада. 2)сколько квадратных метров площади сада занимают яблони...

Популярные вопросы