Определите все пары простых чисел p и натуральных n, для которых 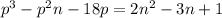$p^{3}-p^{2}n-18p=2n^{2}-3n+1$

Ответы

CuprumJewellier5 15.10.2020 20:32

Преобразуем

p(p^2-pn-18) = (2n-1)(n-1)

То есть правая часть обязана делиться на p, то так как p простое возможно два варианта: либо 2n-1 = p либо n-1 = p

Рассмотрим первый

$(2n-1)((2n-1)^2-(2n-1)n-18) = (2n-1)(n-1)\\4n^2-4n+1-2n^2+n-18 = n-1\\2n^2-4n-16=0\\n^2-2n-8=0\\(n-4)(n+2)=0$

Натуральный корень n=4, при этом 2n-1 = 7 - простое число.

Рассмотрим второй

$(n-1)((n-1)^2-(n-1)n-18) = (2n-1)(n-1)\\n^2-2n+1-n^2+n-18 = 2n-1\\3n+16=0$

Натуральных решений нет

ответ: существует единственная пара n=4, p=7

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

sanekakot 11.05.2021 19:13

maritsumie 11.05.2021 19:13

Найти число если 1) 5% его равны 12 2) 15% его равны 8,4...

malinasch 11.05.2021 19:13

МашаМозг112 11.05.2021 19:12

marija01021 11.05.2021 19:12

решить, 5 класс (математика) Дам лучший ответ и...

Maksim2553 11.05.2021 19:12

kakashka564 11.05.2021 19:12

тати31 11.05.2021 19:12

maxidrom614 11.05.2021 19:12

Серєднє арифметичне 7,2 і 7,4...

fill1337 11.05.2021 19:12

Определите все пары простых чисел p и натуральных n, для которых