Определите вид треугольника, если А(0,7,-3), В(2,-3,2), С(0,3,10)
Другие вопросы по теме Математика
Популярные вопросы
- Мини сочинение-описание, на тему кленовый лист осенью . 3-5 предложений....
2 - 3пломбира декабрь и 7 пломбиров январь стоят вместе 196 рублей, а 7 пломбиров...
2 - Сфактов докажи, что 16 веке произошёл раздел мира и начались колониальные войны?...
1 - Таблица по за 10 класс.первая колонка признаки строения...
2 - Найдите все простые делители числа: а)19, б)54, в)112, г)232, д)46, е)50, ж)58,...
2 - Как ответить на вопрос did you enjoy your holidays...
2 - Записать на языке: 1) остаток от деления числа а на 36 равен 31. чему равен...
2 - Проводница вагона (длина вагона l), движущегося из москвы в питер ,разнесла...
2 - Какие заначения бывают у слов и какие части слова о них сообщяют...
2 - Заслуги и недостатки жана батиста ламарка...
2
остроугольный, разносторонний
Пошаговое объяснение:
Запишем координаты векторов, выходящих из вершины A, отняв от координат конца соответствующие координаты начала:
Найдем их скалярное произведение как сумму произведений соответствующих координат:
∠A — острый
(если скалярное произведение векторов положительное, угол α между ними острый, равное нулю — прямой, отрицательное — тупой. Все из-за множителя cosα, знак которого зависит от величины угла)
Аналогично поступим с векторами, выходящими из вершины B: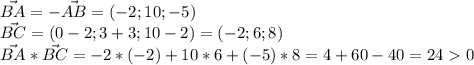
∠B тоже острый
И все те же действия повторим для векторов, выходящих из вершины C:
∠C также острый
Получили, что ΔABC — остроугольный
Наконец найдем длины его сторон, которые совпадают с модулями уже выписанных векторов AB, BC и CA:
Сравнивая длины сторон, приходим к выводу, что ΔABC — разносторонний