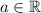Определите при каких значениях параметра а уравнение |x+1|=a²+1 имеет два корня
Другие вопросы по теме Математика
Популярные вопросы
- Число а не делятся на 10 Определите какие из следующих чисел...
2 - 1. Исследуйте модель сотенного квадрата, в которой показано...
1 - Рівні відрізки AB і CD перетинаються в точці O що OA=OD. доведіть...
2 - Дано: Треугольник A B C угол A= B+C угол B= 1|3(дробь) (A+C)...
3 - Немедленно! Пишите правильный ответ, не пишите всякую ерунду,...
1 - 1)4 ¹¾/¹⁷+5⁴/¹⁷2)3 ⁸/¹¹+2⁶/¹¹3)1-¹⁶/²¹4)5-2³/⁸5)8⁴/⁹-3⁷/⁹612¹⁹/⁴⁴-6³⁷/⁴⁴...
2 - 0.6. Решите неравенство: 1) 11x-8,8 4x+5,2; 3) 18,9x - 13,4х...
3 - Это и вправду было как в сказке. Кленовый листья повисли на...
2 - решить задачу по физике 1 курс универ...
3 - Написати коротке єс чому у Франції люблять Наполеона а вся Європа...
3
Заметим, что в правой части уравнения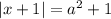 стоит положительное число. Тогда, уравнение равносильно совокупности:
стоит положительное число. Тогда, уравнение равносильно совокупности:
Решая каждое уравнение, получим:
Заметим, что эти корни не могут совпасть, так как в этом случае было бы верным равенство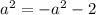 , но соответствующее уравнение
, но соответствующее уравнение 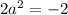 не имеет корней.
не имеет корней.
Значит, уравнение при любых значениях параметра а имеет два корня.
ответ: