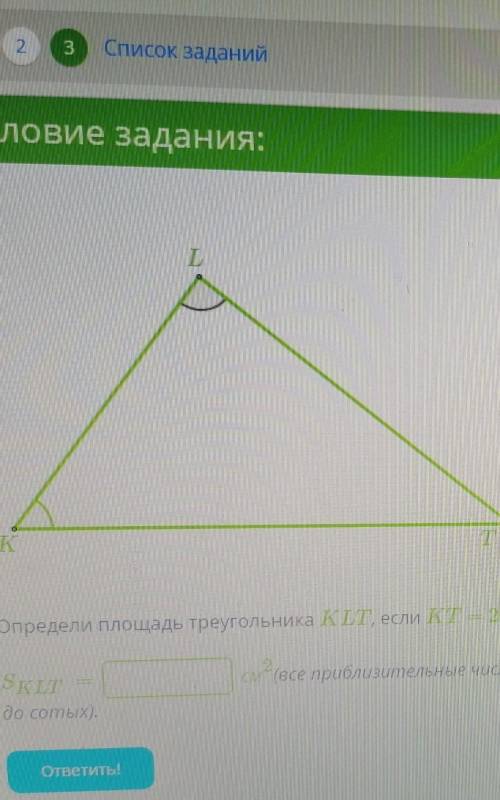
Определите площадь треугольника KLT, если KT=20см,угол K=35, угол L=80 Най­ди­те площадь KLT=? см2(ответ округлить до сотых) ​

Можно ответь

Для нахождения площади треугольника по заданным параметрам (длине стороны и двум углам) мы можем воспользоваться формулой для площади треугольника: S = (1/2) * a * b * sin(C), где a и b - длины сторон треугольника, а C - угол между этими сторонами.

В данном случае, нам даны только длины сторон KT = 20 см и KL (не указана в задаче). Но мы можем найти KL, используя формулу косинусов в треугольнике KLT:

KL^2 = KT^2 + LT^2 - 2 * KT * LT * cos(K)

Подставляем известные значения и рассчитываем KL:

KL^2 = 20^2 + LT^2 - 2 * 20 * LT * cos(35)

KL^2 = 400 + LT^2 - 40 * LT * cos(35)

KL^2 - LT^2 + 40 * LT * cos(35) - 400 = 0

Теперь, зная два угла треугольника (значения K = 35 и L = 80), мы можем рассчитать угол T:

T = 180 - K - L

T = 180 - 35 - 80

T = 65

Таким образом, у нас есть все данные, чтобы рассчитать площадь треугольника KLT.

S = (1/2) * KT * KL * sin(T)

S = (1/2) * 20 * KL * sin(65)

Теперь остается только найти KL, подставить его значение в формулу и рассчитать площадь треугольника KLT.

Надеюсь, данное пошаговое объяснение поможет вам разобраться в задаче и решить ее самостоятельно.