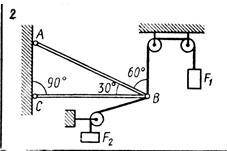
Определить реакции стержней, удерживающих грузы F1=0.3 и F2=0.8 Массой стержней пренебречь.

+
1232121+505+50005++05550

Добрый день! Для ответа на этот вопрос мы можем применить законы Ньютона и равнодействующие силы.

Первым шагом нам нужно разложить силы F1 и F2 на горизонтальную и вертикальную составляющие. Для этого мы можем использовать тригонометрические функции.

Сила F1 направлена вертикально вверх, поэтому ее горизонтальная составляющая равна 0, а вертикальная составляющая равна F1*sin(θ), где θ - угол наклона стержня (θ=30 градусов по изображению).

Сила F2 направлена по диагонали, поэтому мы можем разложить ее на горизонтальную и вертикальную составляющие. Горизонтальная составляющая равна F2*cos(θ), а вертикальная составляющая равна F2*sin(θ).

Теперь мы можем определить реакции стержней. Пусть R1 и R2 - реакции стержней.

Согласно закону Ньютона для вертикального направления:

R1*cos(θ) + R2*cos(θ) = F1*sin(θ) + F2*sin(θ)

R1 + R2 = F1*tan(θ) + F2*tan(θ)

На данный момент мы имеем одно уравнение с двумя неизвестными R1 и R2. Чтобы решить это уравнение, нам нужно второе уравнение.

Согласно закону Ньютона для горизонтального направления:

R1*sin(θ) - R2*cos(θ) = -F2*cos(θ)

R1 = R2*cos(θ) - F2*cos(θ)/sin(θ)

Теперь мы можем подставить это выражение для R1 в первое уравнение:

R2*cos(θ) - F2*cos(θ)/sin(θ) + R2 = F1*tan(θ) + F2*tan(θ)

R2(1 + cos(θ)/sin(θ)) + F2*cos(θ)/sin(θ) = F1*tan(θ) + F2*tan(θ)

R2 = (F1*tan(θ) + F2*tan(θ))/(1 + cos(θ)/sin(θ)) - F2*cos(θ)/sin(θ)

Теперь, используя это выражение для R2, мы можем найти R1, подставив его во второе уравнение.

R1 = R2*cos(θ) - F2*cos(θ)/sin(θ)

Таким образом, мы можем найти значения реакций стержней R1 и R2, используя вышеуказанные формулы.

Обратите внимание, что в нашем решении мы пренебрегли массой стержней, что является упрощением для учебных целей. В реальной жизни влияние массы стержней может быть учтено для получения более точных результатов.