1. Математика
  2. Определить и записать структуру

Определить и записать структуру частного решения у* линейного неоднородного диф уравнения по виду функции f(x): y''-4y'=f(x) a) f(x) = (x-2)^(e4x) b) f(x) = 3cos4x

Nastysha222 Nastysha222    3   24.05.2021 16:57    0

Ответы
dashenkanosova5 dashenkanosova5  23.06.2021 17:00

Найдем общее решение правой части (ОЛДУ)

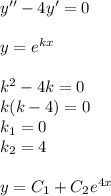
y'' - 4y '= 0 \\ \\ y = {e}^{kx} \\ \\ k {}^{2} - 4k = 0 \\ k(k - 4) = 0\\ k_1 = 0 \\ k_2 = 4 \\ \\ y = C_1 + C_2 {e}^{4x}

а)

y'' - 4y' = (x - 2) {e}^{4x}

y= Ax + B

В общем решении ОЛДУ есть константа без переменной (С1), поэтому многочлен домножаем на х.

y = x(Ax + B) = (A {x}^{2} + Bx)

Также домножаем на е^(4х)

Получаем структуру частного решения:

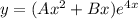
y= (A {x}^{2} + Bx) {e}^{4x}

б)

y ''- 4y' = 3 \cos(4x)

здесь правая часть не имеет пересечений с общим решением ОЛДУ, поэтому стандартный вид частного решения для тригонометрических функций:

y = A \sin(4x) + B \cos(4x)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Мандаринка500 Мандаринка500  30.11.2021 00:54
До іть, будь ласка, не можу розібратися, яку використовувати формулу. Замінюючи приріст функції диференціалом, наближено обчислити...
ladyplahtiy ladyplahtiy  30.11.2021 00:49
Водоём имеет форму квадрата, сторона которого 30/1,2 м. Найдитё длину забора вокруг водоёма....
lika343 lika343  30.11.2021 00:48
Найти площадь параллелограмма...
пух8564 пух8564  30.11.2021 00:47
ПитаняГрупі студентів з 30 чоловік була запропонована контрольна робота з трьох завдань. Перше завдання розв’язали 15 студентів, друге - 13, третє - 12. Перше й друге...
Tuchka087 Tuchka087  30.11.2021 00:47
ВСЕМ ПРИВЕТ С 2 ВАРИАНТОМ. ЗАВТРА ПРАКТИЧЕСКАЯ,НЕ МОГУ ПОНЯТЬ ТЕМУ. В ИНЕТЕ НЕ НАШЛА...
whitepanda1 whitepanda1  30.11.2021 00:43
4. Банк начисляет 10% годовых, внесенная сумма 5000000тг Каким будет вклад через 2 года? [2]...
MikeSandorik MikeSandorik  30.11.2021 00:41
Знайдіть невідомий член пропорції 8:х=2,5:1,25...
Farpli Farpli  30.11.2021 00:32
Найди значение выражения -5,36+2×(-1,25÷2,5-6)...
kill2021 kill2021  30.11.2021 00:29
Знайдіть відношення: 1) 7,2 до 0,18;...
memasov memasov  30.11.2021 00:28
3. Запишите периодическую десятичную дробь в виде обыкновенной: а) 0,(3); Б)- 0,(185) с) -8,(54). d) 3,4(73)...

Популярные вопросы