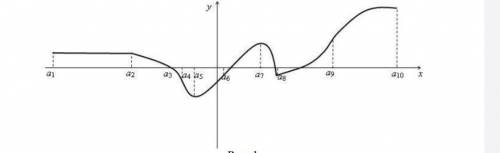
Определить где y"=0 y">0 y"<0 y' не существует​

Для решения данной задачи необходимо использовать график функции y(x).

Чтобы найти значения y"=0, y">0, y"<0 и y' не существует, следует проанализировать поведение функции на каждом участке графика.

1. Определение значений y=0:
Найти точки пересечения графика функции с осью Oy (y-ось), т.е. значения y(x), при которых y=0. Это будет являться корнями уравнения y=0. Визуально на графике это будут точки, в которых график пересекает y-ось.

2. Определение значений y'>0:
Найти интервалы, где график функции возрастает. Возрастание функции означает положительное значение ее производной. Для нахождения интервалов возрастания следует проанализировать участки графика, на которых график строго возрастает (график имеет положительный наклон).

3. Определение значений y'<0:
Найти интервалы, где график функции убывает. Убывание функции означает отрицательное значение ее производной. Для нахождения интервалов убывания следует проанализировать участки графика, на которых график строго убывает (график имеет отрицательный наклон).

4. Определение значений y"=0:
Найти точки пересечения графика производной функции с осью Ox (x-ось), т.е. значения x, при которых y"=0. Это будет являться корнями уравнения y"=0. Визуально на графике это будут точки, в которых график производной функции пересекает x-ось.

5. Определение значений y' не существует:
Найти точки разрыва графика функции, в которых значение производной не существует. Это могут быть точки, в которых график функции имеет вертикальную асимптоту, разрывы первого рода или разрывы второго рода.

Обратите внимание, что для определенных значений x возможны одновременное существование двух или более условий (например, y'=0 и y"=0). Также стоит помнить, что график функции может иметь сложную форму, а его анализ может потребовать дополнительных математических методов.

В данном конкретном случае, на графике изображены две кривые, синяя и оранжевая. Чтобы точно определить значения y=0, y'>0, y'<0 и y"=0, необходимо изучить уравнения этих кривых и их поведение на графике.