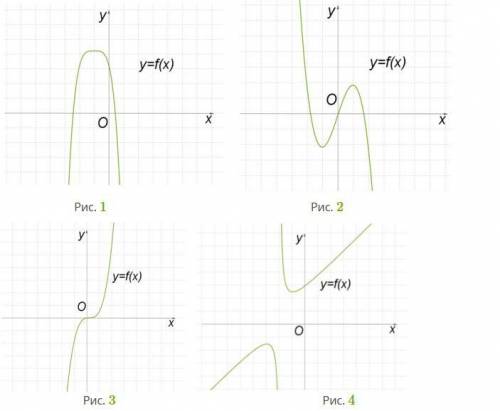
Определи, сколько точек максимума имеют функции, графики которых изображены на рисунках

На первом рисунке график функции имеет одну точку максимума, на втором рисунке график функции не имеет точек максимума, а на третьем рисунке график функции имеет две точки максимума.

Обоснование:

Точка максимума функции - это точка на графике функции, где значение функции достигает наибольшего значения. Чтобы определить, сколько точек максимума имеет функция, нужно найти экстремумы функции, то есть точки, где производная функции равна нулю или не существует.

1. На первом рисунке график функции имеет одну точку максимума. Это можно определить по форме графика - он имеет пик и спускается с обеих сторон от этой точки. Для математического обоснования можно воспользоваться производной функции: если производная функции равна нулю (или не существует) в данной точке и меняет знак с плюса на минус при движении слева направо, то это точка максимума.

2. На втором рисунке график функции не имеет точек максимума. Это можно определить по форме графика - он не имеет никаких пиков или возвышенностей, а только непрерывно убывает или возрастает. Математически это можно проверить, найдя производную функции и установив, что она всегда положительна (функция всегда возрастает) или всегда отрицательна (функция всегда убывает) на всем множестве определения функции.

3. На третьем рисунке график функции имеет две точки максимума. Можно заметить, что функция сначала возрастает до первой точки максимума, затем убывает до второй точки максимума, а затем снова возрастает. Математически это можно проверить, найдя производную функции и установив, что она равна нулю (или не существует) в каждой точке максимума и меняет знак с плюса на минус между этими точками.

Итак, первый рисунок содержит график функции с одной точкой максимума, второй рисунок - график функции без точек максимума, и третий рисунок - график функции с двумя точками максимума.

2

Чтобы построить прямую достаточно 2-х

точек

Пошаговое объяснение: