Окружность проходит через вершины в и с треугольника авс и пересекает ав и ас в точках с1 и в1 соответственно. найдите радиус данной окружности, если угол а =30 градусов, в1с1=5 и площадь треугольника ав1с1 в три раза меньше площади четырехугольника всв1с1.
Ответы
Треугольники ABC и ABC₁ подобны и их площади относятся как 4:1. Значит AC=2AC₁. Значит, для тр-ка ACC1 по теореме косинусов
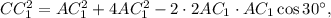 т.е.
т.е. 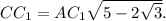 Тогда по теореме синусов для этого же треугольника
Тогда по теореме синусов для этого же треугольника 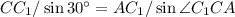 , т.е.
, т.е. 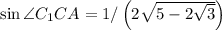 . По теореме синусов для тр-ка B₁CC₁ получаем
. По теореме синусов для тр-ка B₁CC₁ получаем 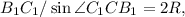 откуда
откуда 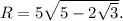
ПОКАЗАТЬ ОТВЕТЫ
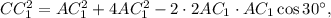 т.е.
т.е. 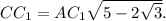 Тогда по теореме синусов для этого же треугольника
Тогда по теореме синусов для этого же треугольника 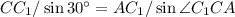 , т.е.
, т.е. 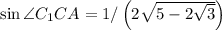 . По теореме синусов для тр-ка B₁CC₁ получаем
. По теореме синусов для тр-ка B₁CC₁ получаем 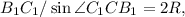 откуда
откуда 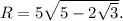
Другие вопросы по теме Математика
Популярные вопросы
- Формула 3-хлорпентаналя очень нужно...
1 - Текстові процесори призначенні для опрацювання документів, що містять ...
1 - Айдағы жасырынбак көркемдегіш куралдар табу кажет тезирек боладыма беремин...
2 - . Оқылым мәтіндері бойынша «FILA» кестесін толтырыңдар. Facts (мәтін-Ideas (мәтіннің...
2 - Здійсніть перетворення,що відбувається за схемою S-SO2-K2SO3...
1 - Хел алгебра 8 клас теорема вієта...
3 - 6. Палка, с которой человек несет груз, приложена к плечу в точке С. Найти массугруза,...
1 - в двухместном палате находятся 2 тяжелобольных, для которых имеется в палате только...
1 - До Московского Князівства увійшлиа) Волиньб) Київщина в) Чернігівщинаг) Переяславщинад)...
3 - Помагитее поис английский 1 и 2...
2