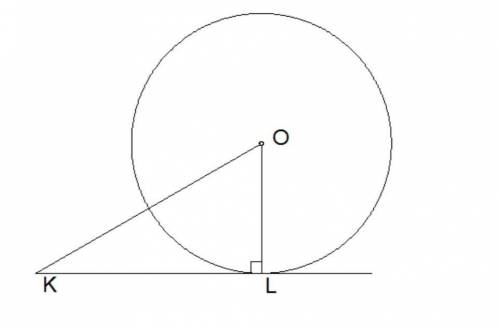
∢ OKL = 30°.
Отрезок касательной
LK = 6,23–√ дм.
Найди длину окружности
C= π дм.
(Если необходимо, ответ округли до сотых
Другие вопросы по теме Математика
Популярные вопросы
- Фонетический разбор слов сошёл,голая...
2 - Кднню защитнека отечества девочки 3 класса купили 40 вездушных шариков. из них...
3 - Известно что mf=30 см me=18 см kf = 22см найдите длину отрезка ke это я в большом...
2 - Собственная скорость голубя равна 55 км/ч. скорость ветра 5,5 км/ч. голубь летел...
3 - На самом ли деле удача сопутствует смелым по слову о полку игореве...
2 - Ккому типу выживания ( избегание, подчинение или сопротивление) мы отнесем : переживание...
2 - Отметьте точку м. проводите лучи мn и мl. какая точка будет начало для этих лучей...
3 - Автобус за 8 ч расстояние 560 км на обратный путь он затратил 7ч на сколько изменилась...
1 - Составить предложения к слову ходячая энциклопедия...
1 - Можно ли садко назвать поэтическим героем?...
1
Из условия задачи, дано:
∢ OKL = 30°
Длина отрезка LK = 6,23 – √ дм
Длина окружности C = π дм
Мы знаем, что в центральном угле, который соответствует данной дуге, его величина равна удвоенной величине соответствующего угла окружности.
То есть, ∢ OKL = 30°, а для этого же угла на окружности по теореме окружности можно записать следующее равенство: Л = 2∢ OKL
Тогда длина дуги Л будет равна:
Л = 2∢ OKL = 2 * 30° = 60°
Также, дана длина отрезка LK = 6,23 – √ дм
Но в условии задачи сказано, что К - середина дуги. Это означает, что отрезок LK является радиусом окружности. Мы знаем, что радиус окружности равен половине длины диаметра, и диаметр в свою очередь равен двум радиусам.
То есть, длина отрезка LK равна половине диаметра окружности.
Таким образом, длина диаметра окружности будет равна:
Д = 2 * LK = 2 * (6,23 – √) дм
Теперь мы можем найти длину окружности, используя формулу для длины окружности:
C = π * Д
C = π * 2 * (6,23 – √)
Используя значение числа π (пи), равное приблизительно 3,14, мы можем вычислить значение длины окружности C, подставляя все значения в формулу.
C = 3,14 * 2 * (6,23 – √)
После подстановки и выполнения вычислений, получим ответ на задачу.