. Очень важно !
Нужно найти точки перегиба функции:
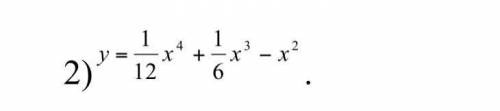
Другие вопросы по теме Математика
Популярные вопросы
- Що наталя миколаївна із твору климко відмовилася обміняти бороданеві на базарі?...
1 - 1) (х^2+1)^2-4х^2= 2) 4у^2-(у-с)^2=...
1 - Решить : підчас спалювання 100кг сірки утворилося 160кг сульфуру (iv) оксиду....
3 - Складіть невеликий текст-опис весняного вечора (5-8 речень) ввести одне безполучникове...
3 - Если бы живые организмы приносили потомство, не превышающее количество родителей,...
1 - Написать анатацию к книге гари потер...
3 - Переводить ocean world: whales whales are the biggest animals in the sea.they...
1 - Определите, в каком из слов пропущенную гласную нельзя проверить ударением....
2 - Составьте предложение из следующих слов и переведите его на язык is influenced,the...
1 - Письменно подтвердите, что во второй половине xvii в. царская власть приобрела...
2
х = -1-√13, х =0, х = -1 + √13
1 2 3
Точки перегиба функции определяются по второй производной функции.
Находим: y' = (4/12)x^3 + (3/6)x^2 - 2x или
y' = (1/3)x^3 + (1/2)x^2 - 2x.
Далее: y'' = (3/3)x^2 + (2/2)x - 2 или y'' = x^2 + x - 2 .
Приравниваем нулю вторую производную.
x^2 + x - 2 = 0, D = 1 - 4*(-2) = 9, √D = +-3.
x1 = (-1 - 3)/2 = -2,
x2 = (-1 + 3)/2 = 1.
ответ: две точки перегиба х1 = -2 и х2 = 1.