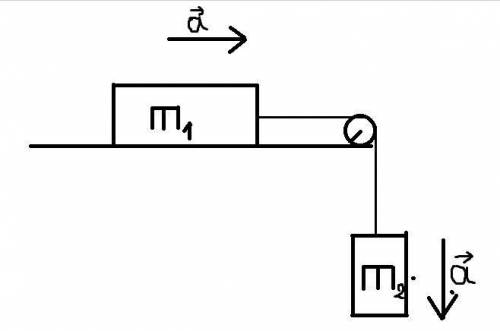
очень подробно написать! Два тела, связанные невесомой нерастяжимой нитью, перекинутой через невесомый неподвижный блок движутся с ускорениями, модули которых 4,5 м\с². Коэффициент трения между телом массой m₁ и горизонтальной поверхностью 0.65. Определите массу первого тела, если масса второго 360 г.

Для решения этой задачи, мы должны разбить её на два этапа: анализ каждого тела отдельно и анализ общей системы.

1) Анализ первого тела:
Давайте назовем первое тело с массой m₁. Вертикальная составляющая ускорения m₁ будет равна ускорению свободного падения g, так как нить невесома и натянута вертикально.

По горизонтали на первое тело воздействует сила трения F₁. Используя второй закон Ньютона (F = m*a), мы можем записать уравнение для данного тела:
m₁ * a₁ = F₁ - F₁тр = F₁ - μ₁*m₁*g, где μ₁ - коэффициент трения.

Учитывая, что модуль ускорения a₁ равен 4,5 м/с² и коэффициент трения μ₁ равен 0,65, мы можем записать силу трения F₁тр = 0,65 * m₁ * g. Подставляя это в уравнение, получим:
m₁ * 4,5 м/с² = F₁ - 0,65 * m₁ * g.

2) Анализ второго тела:
Давайте назовем второе тело с массой m₂ и будем считать, что у него нет вертикального движения. Значит, горизонтальная составляющая ускорения m₂ будет равна модулю ускорения общей системы (предполагается, что горизонтальное ускорение происходит вправо). Таким образом,
a₂ = aᵣ = 4,5 м/с².

Также, на второе тело действует нить с силой натяжения T и сила трения F₂. По горизонтали, мы можем записать уравнение:
m₂ * a₂ = T - F₂тр.

3) Анализ системы:
Теперь, когда мы учли отдельные аспекты каждого тела, давайте рассмотрим систему в целом. Мы знаем, что ускорение системы (аᵣ) равно модулю ускорения каждого тела. То есть, аᵣ = a₁ = a₂ = 4,5 м/с².

На систему также действует нить с силой натяжения T и сила трения F₂. Учитывая это, мы можем написать уравнение:
(m₁ + m₂) * aᵣ = T - F₂, где F₂тр - сила трения на втором теле.

4) Нахождение m₁:
Теперь у нас есть два уравнения, связывающие разные аспекты задачи. Давайте решим их один за другим, чтобы найти массу первого тела.

Из первого уравнения мы получили:
m₁ * 4,5 м/с² = F₁ - 0,65 * m₁ * g.

Теперь, мы можем решить второе уравнение относительно T и F₂ и подставить его в уравнение для системы:
(m₁ + m₂) * 4,5 м/с² = T - F₂.

Подставим значение T в уравнение для первого тела:
(m₁ + m₂) * 4,5 м/с² = (F₁ + F₂тр) - F₂.

Теперь подставим значение F₁ из первого уравнения для первого тела:
(m₁ + m₂) * 4,5 м/с² = (m₁ * 4,5 м/с² + 0,65 * m₁ * g + F₂тр) - F₂.

Заметим, что ускорение aᵣ на всех телах одинаково, а сила трения F₂тр равна μ₂ * m₂ * g. Подставим эти значения в уравнение:
(m₁ + m₂) * 4,5 м/с² = (m₁ * 4,5 м/с² + 0,65 * m₁ * g + μ₂ * m₂ * g) - F₂.

Теперь можно перенести все значения на одну сторону и объединить подобные переменные:
(m₁ + m₂) * 4,5 м/с² - m₁ * 4,5 м/с² - 0,65 * m₁ * g - μ₂ * m₂ * g = -F₂.

Учитывая, что модуль ускорения aᵣ равен 4,5 м/с², коэффициент трения между вторым телом и поверхностью μ₂ равен 0,65, и сила трения F₂тр равна μ₂ * m₂ * g, мы можем упростить уравнение:
m₂ * 4,5 м/с² - 0,65 * m₁ * g - μ₂ * m₂ * g = -F₂.

5) Решение уравнения и нахождение m₁:
Теперь, чтобы решить уравнение относительно m₁, мы должны знать значения массы второго тела m₂ и ускорения свободного падения g, и подставить значения всех переменных в уравнение.

Данные из условия задачи:
- Масса второго тела m₂ = 360 г = 0,36 кг.
- Ускорение свободного падения g = 9,8 м/с².

Подставим эти значения в уравнение:
0,36 кг * 4,5 м/с² - 0,65 * m₁ * 9,8 м/с² - 0,65 * 0,36 кг * 9,8 м/с² = -F₂.

Теперь, остается только решить получившееся уравнение относительно m₁:
1,62 м/с² * m₁ - 2,835 кг * m₁ - 0,22884 кг * м/с² * m₁ = -F₂.

Соберем коэффициенты перед m₁ и перенесем все значения на одну сторону:
(1,62 м/с² - 2,835 кг - 0,22884 кг * м/с²) * m₁ = -F₂.

Теперь мы можем рассчитать значение в скобках:
(1,62 м/с² - 2,835 кг - 0,22884 кг * м/с²) ≈ -1,40816 кг * м/с².

Подставим это значение назад в уравнение и выразим m₁:
-1,40816 кг * м/с² * m₁ = -F₂.
m₁ = -F₂ / (-1,40816 кг * м/с²).

Теперь, нам нужно учитывать, что мы находимся в условиях равнодействующая силы трения на втором теле всегда направлена влево, противоположно направлению движения этого тела. Таким образом, F₂ будет равно μ₂ * m₂ * g. Подставим это значение и рассчитаем m₁:
m₁ = -(μ₂ * m₂ * g) / (-1,40816 кг * м/с²).

Теперь, остается только подставить значения массы второго тела m₂ и ускорения свободного падения g в данное уравнение:
m₁ = -((0,65 * 0,36 кг * 9,8 м/с²) / (-1,40816 кг * м/с²)).

После вычислений, мы получим значение массы первого тела m₁. Ответ должен быть численным значением в килограммах.