ОЧЕНЬ-ОЧЕНЬ НАЙТИ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЮ
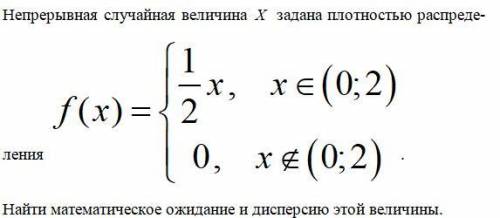
Другие вопросы по теме Математика
Популярные вопросы
- Почему клад был закопан на небольшую глубину?...
3 - Подчеркни слова , которые обозначает действие предмета. цветут...
2 - Ввоздухе запахло весной. : выполнить морфологический разбор слова...
2 - На складе было 30 велосипедов . среди них женских 6 а мужских в...
2 - Разбор предложения: ты возьми книгу в руки и не будет скуки....
3 - Начерти схему к . запиши решение . вычисли ответ. два автомобиля...
2 - Встроке 56 печатных знаков, а на странице-36 строк. сколько печатных...
2 - Задайте по 4 типа вопросов ко всем предложениям. 1. he will read...
1 - Сочинение на тему: в чем смысл жизни человека...
1 - Сочинение о рассказе урок французского . как вы поняли, ваши ощущения...
3
Пошаговое объяснение:
Математическое ожидание для непрерывной случайной величины задается интегралом
Дисперсию можно посчитать по следующей формуле: