ОЧЕНЬ
Найти частное решение ,удовлетворяющие заданному условию:
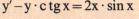
Другие вопросы по теме Математика
Популярные вопросы
- Y=-2x+3(знайти значення функціі якщо значення аргументу =3...
1 - Какое расстояние проедет автомобиль с двигателем мощностью 100 квт и кпд 25%...
3 - Испекли 100 пирожков с капустой ,по 20 штук на каждом противне . а с повидлом...
2 - Напиши слова с уменьшительно-ласкательным значением,используя суффиксы --.выдели...
3 - Решите уравнение: д) 5/4х²-х+1/9=0 в примере- дроби. нужно подробное решение...
2 - Надо 20дм в кубе перевести в метры в кубе, , подалуйста....
1 - 7хлопчиків налили в бочку по 2 відра води кожний. 5 відер води використали...
1 - 1/3х+1/5у=11 3/5х-2у=8 решить линейное уравнение...
1 - Назовите 3 периода освободительного движения ( надо )...
1 - Зробити звукову модель і звуко буквиний аналіз вються...
3
общее решение
частное решение
ответ: у(х)=(x²-π²/4)·Sinx
Пошаговое объяснение: решим сначала однородное уравнение:
y'-уctgx=0
dy/y=ctgx
∫dy/y=∫ctgx dx
lny=∫cosx dx/sinx
lny= ∫d(sinx)/sinx
lny= ln(sinx)+lnC
lny= ln(C·Sinx)
y=C·Sinx
Используем метод вариации произвольной постоянной :
пусть y(x)=C(x)·Sinх, пиши ВК id92240104
тогда y'(x)=C'(x)·Sinх+C(x)·Cosх, подставим значения y(x), y'(x) в данное уравнение:
C'(x)·Sinх+C(x)·Cosх-C(x)·Sinх·Cosx/Sinх=2·x·Sinx
C'(x)·Sinх=2·x·Sinx
C'(x)·Sinх-2·x·Sinx =0
Sinx·(C'(x)-2x)=0 ⇒ C'(x) = 2x ⇒C(x)= x²+C₁ ⇒
Так как у нас у=С(x)·Sinx=(x²+C₁)Sinx
Значит общее решение : у(х)=(x²+C₁)·Sinx
удовлетворяет условию y(π/2)=0 ⇒
y(π/2)= (π²/4+C₁)·Sin(π/2)= (π²/4+C₁)·1= π²/4+C₁ ⇒ π²/4+C₁=0 ⇒
C₁= - π²/4
Тогда частное решение имеет вид: у(х)=(x²-π²/4)·Sinx