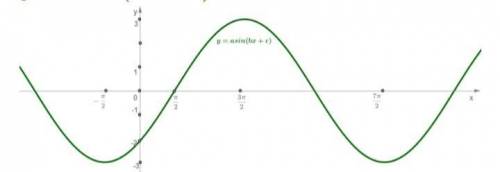
очень надо, Подбери коэффициенты a, b, c так, чтобы на данном рисунке был изображён график функции y=asin(bx+c).
a=?
b=?
c= ?pi/?

Для того, чтобы определить значения коэффициентов a, b и c в уравнении y = a*sin(bx+c), мы должны проанализировать форму графика функции на данном рисунке.

Сначала рассмотрим основные характеристики, которые влияют на форму функции:

1. Амплитуда (a): Амплитуда функции определяет вертикальную высоту колебаний. На данном рисунке амплитуда оценивается примерно 3.

2. Период (T): Период функции определяет расстояние между двумя соседними пиками или впадинами на графике. На данном рисунке период составляет приблизительно 4.

3. Фазовый сдвиг (c): Фазовый сдвиг определяет горизонтальное смещение графика функции относительно начала координат. На данном рисунке график начинается с отметки примерно равной -2.

На основе этих характеристик, давайте определим значения коэффициентов:

1. Значение амплитуды (a): Мы видим, что на графике функции максимальное значение y достигается приблизительно в точке y = 3, а минимальное значение достигается примерно в точке y = -3. Таким образом, амплитуда будет равна половине разности этих значений: a = (3-(-3))/2 = 6/2 = 3

2. Значение периода (T): Мы видим, что на графике функции один полный цикл проходит через 4 единицы по оси x. Так как уравнение sin имеет период 2π, мы можем использовать следующую формулу для определения периода:
T = 2π/b
Из данного уравнения можно найти значение b:
2π/b = 4
2π = 4b
b = 2π/4 = π/2

3. Значение фазового сдвига (c): Мы видим, что график функции начинает свое колебание при x = -2. Таким образом, фазовый сдвиг равен -2.

Итак, значения коэффициентов a, b и c в уравнении y = a*sin(bx+c) для того, чтобы на данном рисунке был изображен график функции, будут следующими:

a = 3
b = π/2
c = -2

Таким образом, уравнение функции, изображенной на данном рисунке, будет y = 3*sin((π/2)x-2).