Объясните как искать градиент и производную по направлению a(вектор) в точке А z = In (10x2 + y2), A (-1;10), a (вектор) = 10 i (вектор) -j (вектор)

Ответы

Whitecat111 25.02.2021 14:21

Пошаговое объяснение:

z = log(10x²+y²)

градиент функции z = f(x,y) это вектор, координатами которого являются частные производные данной функции,

$\displaystyle grad(z) = \frac{\delta z}{\delta x} i+\frac{\delta z}{\delta y} j$

$\displaystyle { \frac{\delta z}{\delta x} =20\frac{x}{10x^2+y^2} }$

$\displaystyle { \frac{\delta z}{\delta y} =2\frac{y}{10x^2+y^2} }$

$grad(z) = \displaystyle \frac{20x}{10x^2+y^2} i+\frac{2y}{10x^2+y^2} j$

теперь градиент в точке А(-1;10)

$grad(z)_A = \displaystyle \frac{20*(-1)}{10(-1)^2+(10)^2} i+\frac{2*10}{10(-1)^2+(10)^2} j=-\frac{2}{11} i+\frac{2}{11} j$

и еще нам понадобится модуль grad(z) в точке А

$\mid grad(z)_A \mid= \displaystyle \sqrt{\bigg ( \frac{\delta z}{\delta x} \bigg)^2+\bigg ( \frac{\delta z}{\delta y} \bigg)^2 }=\sqrt{\bigg ( -\frac{2}{11} \bigg)^2+\bigg ( \frac{2}{11} \bigg)^2 }=\frac{2\sqrt{2} }{11}$

теперь направление вектора-градиента задаётся его направляющими косинусами и мы можем рассчитать эти косинусы

$\displaystyle cos \alpha = \frac{\delta z/\delta x}{\mid grad(z)_A \mid} = -\frac{1}{\sqrt{2} } ;$ $\displaystyle cos \beta = \frac{\delta z/\delta y}{\mid grad(z)_A \mid} = \frac{1}{\sqrt{2} } ;$

так, с градиентом расплевались.

теперь производная по направлению вектора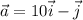 $\dislpaystyle \vec a= 10\vec i-\vec j$

производная в точке А по направлению вектора а(10;-1)

$\displaystyle \frac{\delta z}{\delta a} = \frac{\delta z}{\delta x} cos \alpha +\frac{\delta z}{\delta y} cos\beta$

для косинусов нам понадобится |a|

$\displaystyle \mid a \mid =\sqrt{x^2+y^2} =\sqrt{(-1)^2+10^2} =\sqrt{101}$

$\displaystyle cos \alpha =\frac{x}{\mid a\mid} = \frac{10}{\sqrt{101}} ;$ $\displaystyle cos \beta =\frac{y}{\mid a\mid} = -\frac{1}{\sqrt{101}} ;$

$\displaystyle \frac{\delta z}{\delta a} =\frac{-2}{11} *\frac{10}{\sqrt{101} } +\frac{2}{11}*\frac{-1}{\sqrt{101} } =-\frac{22}{11\sqrt{101} } = -\frac{2\sqrt{101} }{101}$