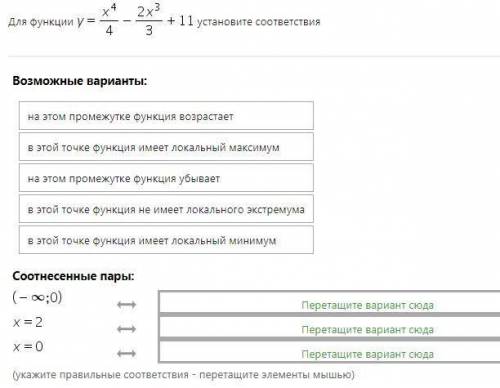
Объясните что куда зачем и как

y`=x³-2x²

y`=0

x³-2x²=0

x²(x-2)=0

x=0; x=2 - точки возможного экстремума.

Применяем достаточное условие экстремума:

если при переходе через точку производная меняет знак с + на -, то это точка максимума, если с - на + , то точка минимума.

Расставляем знак производной:

__-__ (0) __-__ (2) __+__

х=2 - точка локального минимума

Функция  убывает на (-∞;0) и на (0;2)

x=0  не является точкой локального экстремума.

См график для наглядности, почему так