1. Математика
  2. объяснить простым и доступным

объяснить простым и доступным методом, что такое, как использовать и самое главное как находить этот наболевший одз.
объяснит (разжевать) можно на 4ёх уравнениях для наглядности, фото прикрепил.
буду !

messaivi messaivi    3   20.11.2019 00:00    0

Ответы
elank elank  05.08.2020 10:43
) логарифмической функции.

       y=log_{a}x\; ,\; \; x0\; ,\; \; a0\; ,\; a\ne 1\; .

1)\; \; logx+log(x+1)=log6\; \; ,\quad ODZ:\; \left \{ {{x0} \atop {x+10}} \right.\; \left \{ {{x0} \atop {x-1}} \right.\; \; \to \; \; \underline {x0}\\\\log\Big (x\cdot (x+1)\Big )=log6\\\\x(x+1)=6\; \; \to \; \; x^2+x-6=0\; \; \to \; \; x_1=-3\; ,\; x_2=2\; \; (teor.\; Vieta)\\\\x=-3\notin ODZ\\\\Otvet:\; \; x=2\; .

2)\; log_3(x-4)+(log_3(x+2)=log_37\; \; ,\qquad ODZ:\; \left \{ {{x-40} \atop {x+20}} \right.\; \left \{ {{x4} \atop {x-2}} \right.\; \to \; \underline {x4}\\\log_3\Big ((x-4)(x+2)\Big )=log_37\\\\(x-4)(x+2)=7\\\\x^2-2x-8=7\\\\x^2-2x-15=0\\\\x_1=-3\; ,\; x_2=5\; \; (teorema\; Vieta)\\\\x=-3\notin ODZ\\\\Otvet:\; \; x=5\; .

3)\; \; logx+log(2x-3)=\frac{1}{2}\, logx^2\; \; ,\; \; \; ODZ:\; \left \{ {{2x-30} \atop {x0\; ,\; x^20}} \right.\; \left \{ {{x1,5} \atop {x0}} \right.\; \to \; \; \underline {x0}\\\\\star \; \; \frac{1}{2}\, logx^2=\frac{1}{2}\cdot 2\, log|x|=log|x|=logx\; ,\; t.k.\; x0\; \; \star \\\\log\Big (x\cdot (2x-3)\Big )=logx\\\\2x^2-3x=x\\\\2x^2-4x=0\; ,\; \; 2x(x-2)=0\; \; \to \; \; \; x_1=0\; ,\; x_2=2\\\\x=0\notin ODZ\\\\Otvet:\; \; x=2\; .

4)\; \; log(x+8)-log(x-6)=log4,5\; \; ,\; \; ODZ:\; \left \{ {{x+80} \atop {x-60}} \right.\; \left \{ {{x-8} \atop {x6}} \right.\; \to \; \underline {x6}\\\\log\frac{x+8}{x-6}=log4,5\\\\\frac{x+8}{x-6}=\frac{9}{2}\; \; \to \; \; 2x+16=9x-54\; \; \to \; \; \; 7x=70\; \; ,\; \; x=7\in ODZ\\\\Otvet:\; \; x=7\; .

ПОКАЗАТЬ ОТВЕТЫ
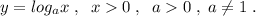
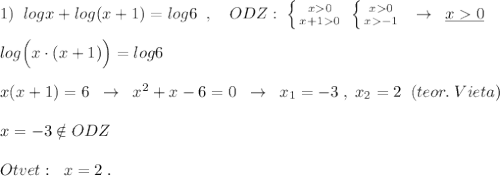
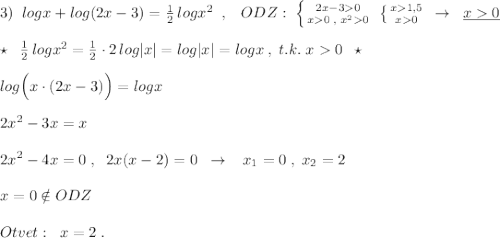
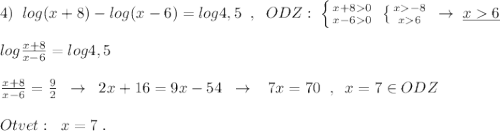
Другие вопросы по теме Математика
Lolopoknhvkcgc Lolopoknhvkcgc  21.04.2021 14:15
130. Запишите числа, используя арабскую систему. а) IIc) Х e) XXIVg) CXLVb) VII d) XI f) CLX ​...
nady2111 nady2111  21.04.2021 14:15
До іть будь-ласка, дуже треба​...
DiDUFC DiDUFC  21.04.2021 14:15
Если масса раствора соли равна 4 кг, то запиши формулу зависимости концентрации раствора от массы соли. По графику зависимости концентрации раствора C от массы соли...
Варёна Варёна  21.04.2021 14:15
Марина Павловна внимательно изучает цены в каталогах, прежде чем пойти за покупками. На сей раз она составила таблицу с ценами на продукты для выпечки из разных магазинов....
rfhbyf23690 rfhbyf23690  21.04.2021 14:14
должен от деталей на креслами с дробным в масштабе 1 / 5 доривнюе 4,8 см я каждую на детали на другому кресло не я пришёл масштаб деревня 1/3​...
ersultanplay ersultanplay  21.04.2021 14:14
мужчина бежал за мышкой когда было между ними расстояние 8 метров. мышка бежала со скоростью 2 м в сек, а мужчина со скоростью 3 м в сек. напишите очень кратко через...
VLADWER5 VLADWER5  21.04.2021 14:13
В четырёх корпусах санатория отдыхают 1260 человек. В первом корпусе расположились 245 человек, во втором56 человек больше, чем в первом, а количество отдыхающихрасположилось...
kety0milka kety0milka  21.04.2021 14:13
Один кот выпил 10 стаканов кофе а другой на 3 больше сколько он выпил? ​...
Ainur0529 Ainur0529  21.04.2021 14:13
18х-5х-2 За теоремою вієта...
jykito28 jykito28  21.04.2021 14:13
Реши задачу. Серики Арман одновременно выехали на велосипедах из по-селка к реке. Через 10 минут Серик, ехавший со скоростью125 м/мин, был у реки. На каком расстоянии...

Популярные вопросы