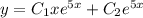Общее решение линейного дифференциального уравнения y''-10*y'+25*y=0 имеет вид
Другие вопросы по теме Математика
Популярные вопросы
- Найдите значение выражений: 1)к+3/4 если к=5/6 2)9/10-к если к-1/6...
1 - Сочинение королевич елисей в поисках невесты...
2 - Числа x и y являются иррациональными числами. определите, какое из утверждений верно...
2 - Язык рабочая тетрадь ваулина модуль 3 стр19 2...
1 - Сочинение по обществознанию на тему почему я люблю свою родину...
2 - Надо какие из точек а ( 1; 29/14 ); в ( 0; 4/7 ); с ( 1; 13/14 ); d ( -2; -17/7...
3 - Осуществить следующие превращения для реакций составьте молекулярные и ионные уравнения...
2 - Предложения словами to и of на нужно. заранее...
3 - 102,8км - 100% ? км - 75% как решить...
2 - Распредели слова по столбикам. в первый записывай слова с орфограммой в приставке,...
2
Поскольку автор задания помещает задачу, которая решается строго по теории, делаю вывод, что он эту теорию не знает. Угадываем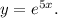 Ну хорошо, не умеем угадывать, характеристическое уравнение не знаем. Выведем его. Ищем решение в виде
Ну хорошо, не умеем угадывать, характеристическое уравнение не знаем. Выведем его. Ищем решение в виде 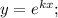 задача подобрать подходящее значение k.
задача подобрать подходящее значение k. 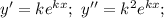 подставляем в уравнение и сокращаем на
подставляем в уравнение и сокращаем на 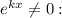
k²-10k+25=0; k=5. К сожалению, подходит только одно значение k, но нам и его хватит. Делаем замену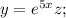 z - новая неизвестная функция.
z - новая неизвестная функция.
ответ: