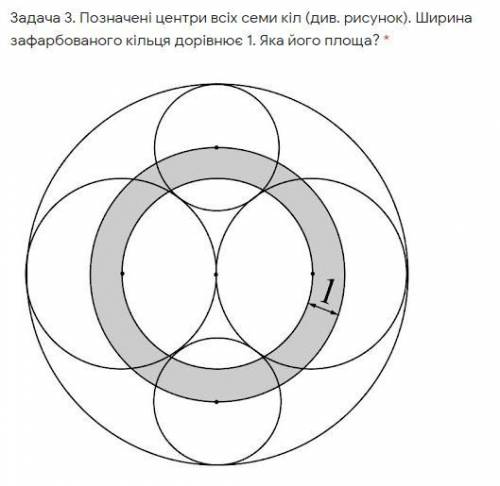
Обозначенные центры всех семи окружностей. Ширина окрашенного кольца равна 1. Какова его площадь?

ответ: 7π

Пошаговое объяснение:

Пусть радиус окружности внутри кольца равен R, в снаружи R+1, соответственно, а расстояние от центра малой окружности до центра большей окружности равно x (из четырех окружностей ,касающихся внутренним образом cамой большой окружности), тогда радиус самой большой окружности можно определить двумя :

2R или R+1 + x - R = x+1, то есть

2R = x+1

x = 2R-1

x^2 = (2R-1)^2

По теореме Пифагора:

x^2 = R^2 + (R+1)^2

Откуда:

R^2 + (R+1)^2 = (2R-1)^2

2R^2 -6R = 0

R≠0

R - 3 = 0

R = 3

Площадь кольца:

S = π( (R+1)^2 - R^2) = π(4^2 - 3^2) = 7π