Объем правильной пирамиды, в основании которой квадрат со стороной 2см, а боковое ребро 3√2 см
Другие вопросы по теме Математика
Популярные вопросы
- Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник...
2 - Иза чего сазтрелиле Магжана Жумабаева...
3 - Что быстрее испортится вишневое варенье или вишневый сок (стоят на столе)...
1 - Выполните задание в тетради следуя алгоритму. Полученные названия запишите в...
2 - На автозаправці перший водій залив у бак 25 л бензину, а дру- гий- 40 л такого...
1 - көмектесіңіздерші өтінемм берем...
1 - Илле-иле, итте-ите, телле-теле, тынны-тыны, тарттык-тартык, киттек-китек, каттык-катык,...
1 - 9. По карте на рисунке 36 определите суммарную солнечную радиацию для десяти...
2 - написать рассказ 100-150 слов на английском языке. PlanIntroductionPara 1:set...
2 - У чому проявляються відмінності економіки країн Азії від Європейського регіону?...
2
5,33 см³.
Пошаговое объяснение:
Объем правильной четырехугольной пирамиды:
V = 1/3 * h * S(основания)
Найдём диагональ основания (по т. Пифагора):
1/2 диагонали основания равна: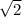 (см)
(см)
Найдём высоту пирамиды (по т. Пифагора):
Найдём площадь основания:
S(основания) = 2 * 2 = 4 (см²)
Найдём объём пирамиды:
V = 1/3 * 4 * 4 ≈ 5,33 (см³)