1. Математика
  2. Обчислити площу фігури

Обчислити площу фігури обмежену лініями y=x в квадрате+2 y=4-x в квадрате

Sofa8412 Sofa8412    2   22.05.2019 08:30    1

Ответы
DEGoP DEGoP  17.06.2020 12:29

\\x^2+2=4-x^2\\ 2x^2=2\\ x^2=1\\ x=-1 \vee x=1\\\\ \int \limits_{-1}^14-x^2-(x^2+2)\, dx=\\ \int \limits_{-1}^1-2x^2+2\, dx=\\ -2\int \limits_{-1}^1x^2-1\, dx=\\ -2\Big[\frac{x^3}{3}-x\Big]_{-1}^1=\\ -2(\frac{1^3}{3}-1-(\frac{(-1)^3}{3}-(-1))=\\ -2(\frac{1}{3}-1-(-\frac{1}{3}+1))=\\ -2\cdot(\frac{2}{3}-2)=\\ -\frac{4}{3}+4=\\ -\frac{4}{3}+\frac{12}{3}=\\ \frac{8}{3}

 


Обчислити площу фігури обмежену лініями y=x в квадрате+2 y=4-x в квадрате
ПОКАЗАТЬ ОТВЕТЫ
abilgaziev1 abilgaziev1  17.06.2020 12:29

Построим графики функций y(1) = x^2 + 2 и y(2) = 4 - x^2

Получились параболы, которые пересекаются в точках -1 и 1 по иксу. Значит будем искать площадь фигуры на промежутке [-1;1] - пределы интегрирования

В данном случае будем y(2) - y(1)

S =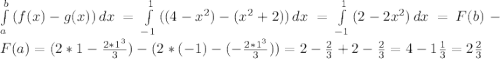 \int\limits^b_a {(f(x) - g(x))} \, dx = \int\limits^1_{-1} {((4 - x^2) - (x^2 + 2))} \, dx = \int\limits^1_{-1} {(2 - 2x^2 )} \, dx = F(b) - F(a) = (2 * 1 - \frac{2 * 1^3}{3}) - (2 * (-1) - (-\frac{2 * 1^3}{3})) = 2 - \frac{2}{3} + 2 - \frac{2}{3} = 4 - 1\frac{1}{3} = 2\frac{2}{3} ед^2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kosorotovslavik kosorotovslavik  30.01.2022 00:07
Запиши с дроби, какую часть метра составляет 29 см...
Mika123123 Mika123123  30.01.2022 00:07
1.11. У трикутнику ABC sinB = 0,2, sinc = 0,4, b = 3 см. Знай- діть с. А) 1,5 см; Б) 4 см; B) 2 см; Г) 6 см....
Ardashelovna Ardashelovna  30.01.2022 00:08
Спростіть вираз і знайдіть його значення: 7,44 + а + (-3,5) + (-5,44) + (-12,5) + b, якщо а = 9,6, b = -5,7....
2008анна22031 2008анна22031  30.01.2022 00:11
Ребят ХАЛЯВНЫЕ __ но только после задания...
diana02lili diana02lili  30.01.2022 00:15
6.при каких значениях букв равенства будут верными? 1)z+z=z2)s•s=s3)d•0=04)1235•c=c5)728•k=k6)987.540:f=987.5407)n•458=458•n8)123.456•m=09)2•b=b+4586 )ДАМ 100 ОЧКОВ!!...
lboik lboik  30.01.2022 00:17
ОЧЕНЬ ЕСЛИ НЕПРАВЕЛЬНО ДАЮ ЖАЛОБУ1. Накресліть координатну пряму, за одиничний вiдрiзок вiзьмiть 2 клітинки зошита. Позначте на нiй: 1) A(2), B(-3,5), C(-1), D(-2). 2) Точку К(-) i...
znasta745 znasta745  30.01.2022 00:17
На фабрике при экономном раскрое сберегли на каждом из 96 пальто по 12 см ткани и на каждом из костюмов по 13 см ткани . Сколько всего см ткани было сэкономлено ?...
133fdsf7za 133fdsf7za  30.01.2022 00:18
Найти b, если график функции у=kx+b проходит через точку E (-2, 1)...
12345678910АБ2261784 12345678910АБ2261784  30.01.2022 00:20
проверь верно или неверно каждое равенство 1/4 = 25/100 4/8=36/40 1/125=8/1000 1/600=60/3600 32/48=2/3 64/32=8/3...
svetik040201p01o4x svetik040201p01o4x  30.01.2022 00:21
Какая часть фигуры изображены на рисунке 12 закрашена а какая не закрашенная 5класс...

Популярные вопросы