Обчислити площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює 8√2 см і нахилена до основи під кутом 45°

ABCDA₁B₁C₁D₁ - правильная четырёхугольная призма с основаниями ABCD и A₁B₁C₁D₁ .

Основания это квадраты т.к. призма прав., так же боковые рёбра перпендикулярны основаниям. Значит боковые грани это равные прямоугольники.

D₁B = 8√2 см.

В ΔD₁DB:

∠D₁DB = 90°; ∠D₁BD = 45° т.к. DB это проекция D₁B на основание ABCD; значит ∠DD₁B = 90°-45° = 45°.

ΔD₁DB - прямоугольный и равнобедренный с гипотенузой 8√2 см, поэтому катеты DD₁ и DB равны 8√2÷√2 = 8см.

В квадрате ABCD диагональ равна 8см, значит стороны равны 8÷√2 = 4√2 см.

см².

S(бок) = 4·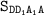 = 4·32√2 = 128√2 см².

ответ: 128√2 см².