Обчислить значение тригонометрических функций, если tg∝=5, π<∝<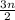
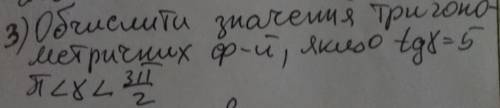
Другие вопросы по теме Математика
Популярные вопросы
- Коли почалася реалізація заходів непу в Україні? А 1920 р.в 1923 р.2Б 1922...
1 - ответьте на вопросы к байке....
1 - 1. ANTYGONA ЯК ТРАГІЧНА ГЕРОЇНЯ - НАПИШИ, ЯК ти РОЗУМІЄШ ПОНЯТТЯ ТРАГІЧНОГО...
1 - а) ( х — 6 )• ( х – 5) = 0 б) 3 • ( х – 2 ) = 0 в) 7 х • ( 4х – 9 ) = 0 Решите...
1 - Дуже потрібга до До 20 г розчину сульфатної кислоти з масовою часткою 4,9 %...
1 - хелп , у меня 5 минут На фото...
1 - Х= -25+25tx=50 - 25tt -? x( t) - ?...
1 - Поставьте артикли, где это необходимо Where immunity to … particular disease...
3 - Маса газу розширюється при початковому тиску p1,бар і почтковій температурі...
3 - Які риси романтичного героя притаманні байронівському Прометеєві?...
3
угол принадлежит 3 четверти, синус, косинус отрицательные, котангенс положительный
по формуле: