1. Математика
  2. Обчисліть площу плоскої фігури,

Обчисліть площу плоскої фігури, обмеженої лініями y=-1/x y=x^2 y=x^2/8

Max70777 Max70777    2   30.05.2023 23:45    0

Ответы
Kate7779393727 Kate7779393727  30.05.2023 23:46

Пошаговое объяснение:

Фигура ограничена линиями $y=-1/x$, $y=x^2$ и $y=x^2/8$.

Точки пересечения графиков можно найти, решив систему уравнений:

\begin{cases}

y = -\frac{1}{x}

y = x^2

y = \frac{x^2}{8}

\end{cases}

Первые два уравнения можно решить методом подстановки:

$$

-\frac{1}{x} = x^2 \Rightarrow x^3 = -1 \Rightarrow x = -1$$

Тогда $y = -1/(-1) = 1$, и точка пересечения первых двух графиков имеет координаты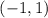 $(-1, 1)$

1 = \frac{x^2}{8} \Rightarrow x = \pm 2\sqrt{2}$$

Таким образом, точки пересечения всех трех графиков имеют координаты $(-1, 1)$ и $(2\sqrt{2}, 2)$

Площадь фигуры можно найти, разбив ее на две части: треугольник и фигуру, ограниченную кривыми $y=x^2$ и $y=x^2/8$

Площадь треугольника равна:

S_{\text{треугольника}} = \frac{1}{2} \cdot 2\sqrt{2} \cdot (2 - 1) = \sqrt{2}$$

Площадь фигуры между кривыми $y=x^2$ и $y=x^2/8$ можно найти, вычислив интеграл:

S_{\text{фигуры}} = \int_{-\sqrt{2}}^{\sqrt{2}} \left(x^2 - \frac{x^2}{8}\right) dx = \frac{15}{8} \sqrt{2}$$

Таким образом, общая площадь фигуры равна:

S = S_{\text{треугольника}} + S_{\text{фигуры}} = \sqrt{2} + \frac{15}{8} \sqrt{2} = \frac{23}{8} \sqrt{2}$$

ответ: $\frac{23}{8} \sqrt{2}$

![graph](https://i.imgur.com/5JZJZJL.png)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kitrfjhhru kitrfjhhru  25.03.2019 10:16
Решите по действиям , ! (-0.25-3/4-1/2)*(-0.2)+3.9...
кирилл5775065421423 кирилл5775065421423  25.03.2019 10:17
Буду вам , если сможете решить данные . не обязательно все, хотя бы штучек 3-5 (8-ое не трогайте)заранее •^•​...
нету36 нету36  25.03.2019 10:21
Сколько в твоей комнате.стен,углов,дверей,окон​...
gerasi1 gerasi1  25.03.2019 10:23
На 3 полках стояло 640книг на 1 полке и второй было 426 книг, а на второй и третьей 397книг. сколько книг стояло на каждой полке?...
NyushaLove NyushaLove  25.03.2019 10:26
Разложите на множители, 1)12ab-18b^{2}2) 21x^{7} -7x^{4} 3) 8x-8y+ax-ay...
DashaKhodenkova DashaKhodenkova  25.03.2019 10:27
Найти производную и экстремум функции: y=|x-4| с решением, ....
mamatvoeymamy mamatvoeymamy  25.03.2019 10:30
Исследуйте функцию и постройте её грфик x^3/(x^2-x+1) пункты исследования: 1)найти область определения ф-ции, интервалы непрерывности, точки разрыва ф-ции 2)чётность и нечётность...
тимур623 тимур623  25.03.2019 10:30
3. какой наибольший остаток может получится при делении числа на 42? а) 41в) 39c) 42d) 43​...
dddddq dddddq  25.03.2019 10:33
Во сколько раз 5900 больше 100...
missanna00 missanna00  25.03.2019 10:33
4. анель младше адели, а адель младше аиданы.айару самая младшая.кто самый старший? a) анельb) айданаc) адельd) айару​...

Популярные вопросы