Обчисліть площу фігури, обмежуної лініями y=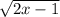 , y=0 , x=5
, y=0 , x=5
Другие вопросы по теме Математика
Популярные вопросы
- Согласно французского просветителя ж.ж.руссо общество: 1) ребенку...
3 - Главная деятельность школьника а)игра б)учение в)труд...
3 - Уэтого растения твёрдый каменный ствол,его корни уходят глубоко...
2 - Напишите уравнения реакций и укажите тип реакций: а) ch2 = ch...
2 - Пример пяти заимствованных слов, их обозначение на язык, и из...
2 - Всоставе сплава содержится 27.3г серебра ,что составляет 0,35...
2 - 4. укажите разряды союзов, употреблённых в предложении: я подумал,...
2 - Мужчина rh- с ав(4) гр.кр. женился на женщине rh+, имеющей кровь...
1 - Ежемесячные доходы фирмы составляет 720 рублей а расходы 500 800...
3 - Переведите на язык: 1) лиза спала когда я вошел в комнату. 2)...
2
Пересечение с ОХ: