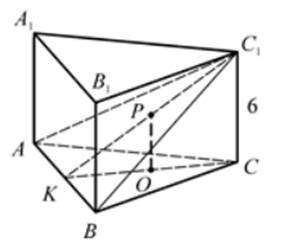
O-центр треугольника ABC, OP||CC1, CC1=6, AB=1/2 OP. Найдите Sбок.
С решением !

Добрый день! Рассмотрим данный вопрос пошагово.

1. Пусть О - это центр треугольника ABC, а OP || CC1, как указано в условии.

2. Также из условия известно, что CC1 = 6 и AB = 1/2 * OP.

3. Для того чтобы найти Sбок, мы должны знать значения всех сторон треугольника ABC.

4. По определению ординаты центра окружности, точка О находится на пересечении биссектрис треугольника.

5. Поэтому, мы можем сказать, что ОС = ОC1, где С - это точка пересечения биссектрисы треугольника, а С1 - точка на линии OP, такая, что CC1 || OP.

6. Поскольку CC1 = 6, то ОС = ОС1 = 6.

7. Обратимся к треугольнику АВО. Мы знаем, что AB = 1/2 * ОР. Значит, AB = 1/2 * 6 = 3.

8. Теперь у нас есть длины всех сторон треугольника ABC: AC = AB + BC = 3 + 6 = 9, BC = CC1 = 6 и AB = 3.

9. Чтобы найти площадь треугольника ABC, мы можем воспользоваться формулой площади Герона или формулой площади прямоугольного треугольника.

10. В данном случае, треугольник ABC является прямоугольным, так как Угол ВАС является прямым углом. Поэтому мы можем использовать формулу площади прямоугольного треугольника: S = (AB * BC) / 2.

11. Подставим значения сторон треугольника в формулу: S = (3 * 6) / 2 = 18 / 2 = 9.

Таким образом, площадь треугольника ABC равна 9.