Нужно подробное объяснение и в правильной четырёхугольной пирамиде со стороной основания 6см, проведена апофема 3 корня из 2см. найдите боковую поверхность пирамиды.
Другие вопросы по теме Математика
Популярные вопросы
- Преобразуйте в произведение: 1) 1 + 2 cosa 2)1 + sina + cosa...
3 - Образующая конуса составляет с высотой угол а. найти боковую поверхность конуса,если...
3 - Из двух сёл одновременно навстречу друг другу выехали машина со скоростью 66 км/ч...
3 - Уприлагательного в сосновом(лесу) определить падеж...
2 - Основание пирамиды – прямоугольник со сторонами 6см и 8 см. высота пирамиды равна...
3 - Между двумя плоскими зеркалами, расположенными параллельно друг другу, находится...
2 - Сочинение-рассуждение на тему зимой в лесу...
2 - Вкаких частях света находятся: 1)гималаи 2)джомолунгма 3)кавказ 4)ливанские горы...
3 - Последовательность (xn) - прогрессия. найдите: а)x1, если x8 = -128, q = -4 б)q,...
1 - Нужно! реакции в полной ионной форме уксусной кислоты с: металлом,с оксидом метала,...
2
Решение в приложении:
ответ:апофема в правильной пирамиде - отрезок между вершиной и серединой стороны основания. Боковая грань пирамиды - равнобедренный треугольник. Апофема в нем является высотой. Площадь равнобедренного треугольника - 1/2 произведения основания и высоты. Значит, площадь одной боковой грани = 1/2*6*«три корня из 2». В пирамиде четыре одинаковые боковые грани, значит, полная боковая поверхность=площадь одной грани*4
S=4*1/2*6*3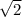
Пошаговое объяснение:
Для начала, вспомним, что апофемой пирамиды называется отрезок, проведенный из вершины пирамиды к центру основания, и он является высотой боковой грани пирамиды.
Дано, что апофема пирамиды равна 3 корня из 2 см. Известно также, что сторона основания пирамиды равна 6 см.
Четырехугольная пирамида имеет четыре боковые грани, которые являются треугольниками. Для того, чтобы найти боковую поверхность пирамиды, нам надо найти площади всех боковых граней и сложить их.
Найдем площадь одной боковой грани пирамиды. Для этого рассмотрим треугольник, образованный апофемой, стороной основания пирамиды и боковой гранью (это прямоугольный треугольник).
Для начала найдем высоту этого треугольника. Мы знаем, что это апофема, которая равна 3 корня из 2 см. А основание треугольника - это сторона основания пирамиды, которая равна 6 см. Используя теорему Пифагора, можем найти высоту треугольника:
высота^2 + половина основания^2 = апофема^2
высота^2 + 3^2 = (3 корня из 2)^2
высота^2 + 9 = 2 * 2
высота^2 + 9 = 4
высота^2 = 4 - 9
высота^2 = -5
Нам пришло отрицательное число при вычислениях, что невозможно в реальности. Из этого мы можем сделать вывод, что проведенная апофема некорректна для данной четырехугольной пирамиды. Если бы у нас были корректные данные, мы могли бы продолжить и решить задачу, но в данном случае мы не можем найти боковую поверхность пирамиды.
В результате, мы не можем ответить на данный вопрос, так как полученные изначально данные не соответствуют реальности или правильным рассуждениям.